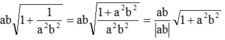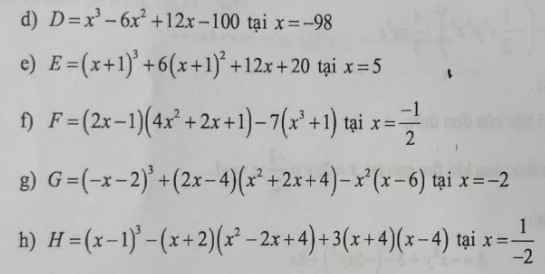
d: \(D=x^3-6x^2+12x-100\)

\(=x^3-6x^2+12x-8-92\)

\(=\left(x-2\right)^3-92\)

Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)

e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)

\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)

\(=\left(x+1+2\right)^3\)

\(=\left(x+3\right)^3\)

Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)

f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)

\(=\left(2x\right)^3-1^3-7x^3-7\)

\(=x^3-8\)

Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)

\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)

\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)

\(=-2x^3-12x-8+2x^3-16=-12x-24\)

Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)

h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)

\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)

\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)

\(=3x-57\)

Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)

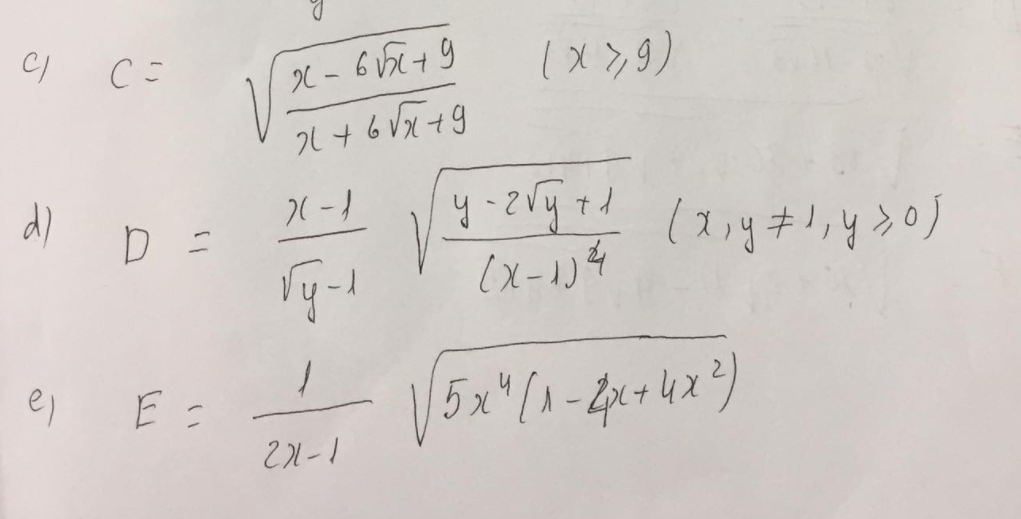
\(C=\sqrt{\dfrac{x-6\sqrt{x}+9}{x+6\sqrt{x}+9}}=\sqrt{\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+3\right)^2}}=\dfrac{\left|\sqrt{x}-3\right|}{\sqrt{x}+3}\)

Vì \(x\ge9\Rightarrow\sqrt{x}\ge3\Leftrightarrow\sqrt{x}-3\ge0\)

\(\Rightarrow C=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)

\(D=\dfrac{x-1}{\sqrt{y}-1}.\sqrt{\dfrac{y-2\sqrt{y}+1}{\left(x-1\right)^4}}\) (\(x;y\ne1;y\ge0\))

\(=\dfrac{x-1}{\sqrt{y}-1}.\dfrac{\sqrt{\left(\sqrt{y}-1\right)^2}}{\left(x-1\right)^2}=\dfrac{\left|\sqrt{y}-1\right|}{\left(\sqrt{y}-1\right)\left(x-1\right)}\)

TH1: \(\sqrt{y}-1>0\Leftrightarrow y>1\)

\(\Rightarrow D=\dfrac{\sqrt{y}-1}{\left(\sqrt{y}-1\right)\left(x-1\right)}=\dfrac{1}{x-1}\)

TH2:\(\sqrt{y}-1< 0\Leftrightarrow0\le y< 1\)

\(\Rightarrow D=\dfrac{-\left(\sqrt{y}-1\right)}{\left(\sqrt{y}-1\right)\left(x-1\right)}=\dfrac{-1}{x-1}\)

Vậy...

\(E=\dfrac{1}{2x-1}.\sqrt{5x^4\left(1-4x+4x^2\right)}\) 

\(=\dfrac{1}{2x-1}\sqrt{5x^4\left(2x-1\right)^2}=\dfrac{\sqrt{5}x^2\left|2x-1\right|}{2x-1}\)

TH1: \(2x-1>0\Leftrightarrow x>\dfrac{1}{2}\)

\(\Rightarrow E=\dfrac{\sqrt{5}x^2\left(2x-1\right)}{2x-1}=\sqrt{5}x^2\)

TH2:\(2x-1< 0\Leftrightarrow x< \dfrac{1}{2}\)

\(\Rightarrow E=\dfrac{-\sqrt{5}x^2\left(2x-1\right)}{2x-1}=-\sqrt{5}x^2\)

Vậy...

c)

\(C=\sqrt{\dfrac{x-6\sqrt{x}+9}{x+6\sqrt{x}+9}}=\sqrt{\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+3\right)^2}}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)

d)

\(D=\dfrac{x-1}{\sqrt{y}-1}.\sqrt{\dfrac{y-2\sqrt{y}+1}{\left(x-1\right)^4}}=\dfrac{x-1}{\sqrt{y}-1}.\dfrac{\left|\sqrt{y}-1\right|}{\left(x-1\right)^2}=\dfrac{\left|\sqrt{y}-1\right|}{\left(\sqrt{y}-1\right)\left(x-1\right)}\)

e)

\(E=\dfrac{1}{2x-1}.\sqrt{5x^4\left(1-4x+4x^2\right)}=\dfrac{1}{2x-1}.\sqrt{5x^4.\left(2x-1\right)^2}=\dfrac{1}{2x-1}.\sqrt{5}x^2.\left|2x-1\right|\)

\(1,\dfrac{\sqrt{27\left(x-5\right)^2}}{\sqrt{3}}\left(dkxd:x\ge5\right)\)

\(=\dfrac{\sqrt{27}.\sqrt{\left(x-5\right)^2}}{\sqrt{3}}\)

\(=\dfrac{\sqrt{3}.\sqrt{3^2}.\left|x-5\right|}{\sqrt{3}}\)

\(=3\left(x-5\right)\)

\(=3x-15\)

\(2,\dfrac{\sqrt{\left(x-4\right)^2}}{\sqrt{9\left(x-4\right)^2}}\left(dkxd:x< 4\right)\)

\(=\dfrac{\left|x-4\right|}{\sqrt{9}.\left|x-4\right|}\)

\(=\dfrac{1}{\sqrt{3}^2}\)

\(=\dfrac{1}{3}\)

\(1,\dfrac{\sqrt{27\left(x-5\right)^2}}{\sqrt{3}}\\ =\dfrac{\sqrt{27}.\sqrt{\left(x-5\right)^2}}{\sqrt{3}}\\ =\dfrac{3\sqrt{3}.\left|x-5\right|}{\sqrt{3}}=3.\left(x-5\right)=3-15\\ 2,\dfrac{\sqrt{\left(x-4\right)^2}}{\sqrt{9\left(x-4\right)^2}}\\ =\dfrac{\left|x-4\right|}{\sqrt{9}.\sqrt{\left(x-4\right)^2}}\\ =\dfrac{\left|x-4\right|}{\sqrt{9}.\left|x-4\right|}=\dfrac{4-x}{3.\left(4-x\right)}=\dfrac{1}{3}\)

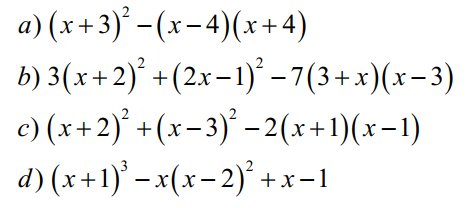
`@` `\text {Ans}`

`\downarrow`

`a)`

\((x+3)^2 - (x-4)(x+4)\)

`= (x^2 + 6x + 9) - (x^2 + 4x - 4x - 16)`

`= x^2 + 6x + 9 - (x^2 - 16)`

`= x^2 + 6x + 9 - x^2 + 16`

`= 6x + 25`

`b)`

\(3(x+2)^2 + (2x-1)^2 - 7(3+x)(x-3)\)

`= 3(x^2 + 4x + 4) + (4x^2 - 4x + 1) - 7(x^2 - 9)`

`= 3x^2 + 12x + 12 + 4x^2 - 4x + 1 - 7x^2 + 63`

`= (3x^2 + 4x^2 - 7x^2) + (12x - 4x) + (12 + 1 + 63)`

`= 8x + 76`

`c)`

\((x+2)^2 + (x-3)^2 - 2(x+1)(x-1)\)

`= (x^2 + 4x + 4) + (x^2 - 6x + 9) - 2(x^2 - 1)`

`= x^2 + 4x + 4 + x^2 - 6x + 9 - 2x^2 + 2`

`= (x^2 + x^2 - 2x^2) + (4x - 6x) + (4 + 9 + 2)`

`= -2x + 15`

`d)`

\((x+1)^3 - x(x-2)^2 + x - 1\)

`= (x^3 + 3x^2 + 3x + 1) - x(x^2 - 4x + 4) + x - 1`

`= x^3 + 3x^2 + 3x + 1 - x^3 + 4x^2 - 4x + x - 1`

`= (x^3 - x^3) + (3x^2 + 4x^2) + (3x - 4x + x) + (1-1)`

`= 7x^2 `

`@` `\text {Kaizuu lv uuu}`

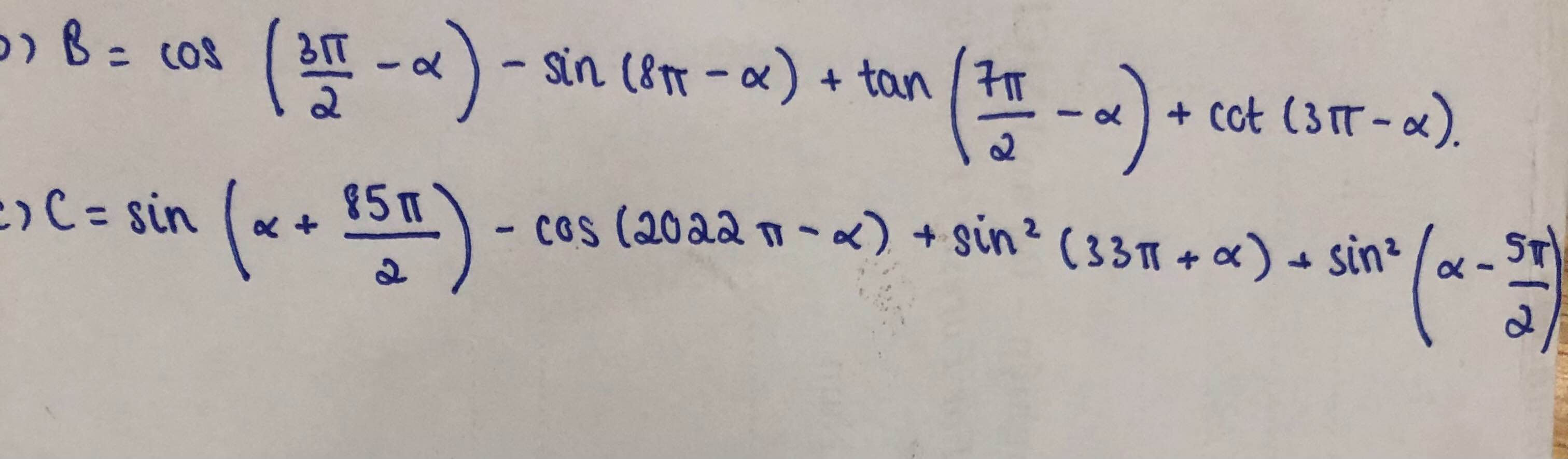
\(B=cos\left(\pi+\dfrac{\pi}{2}-a\right)-sin\left(8\pi-a\right)+tan\left(3\pi+\dfrac{\pi}{2}-a\right)+cot\left(3\pi-a\right)\)

\(=-cos\left(\dfrac{\pi}{2}-a\right)-sin\left(-a\right)+tan\left(\dfrac{\pi}{2}-a\right)+cot\left(-a\right)\)

\(=-sina+sina+cota-cota=0\)

\(C=sin\left(a+\dfrac{\pi}{2}+42\pi\right)-cos\left(2022\pi-a\right)+sin^2\left(33\pi+a\right)+sin^2\left(a-\dfrac{\pi}{2}-2\pi\right)\)

\(=sin\left(a+\dfrac{\pi}{2}\right)-cosa+sin^2a+sin^2\left(\dfrac{\pi}{2}-a\right)\)

\(=cosa-cosa+sin^2a+cos^2a=1\)

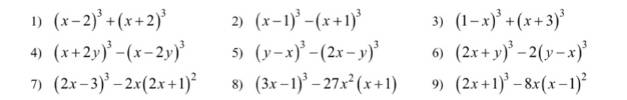
1: =x^3-6x^2+12x-8+x^3+6x^2+12x-8

=2x^3+24x

2: =x^3-3x^2+3x-1-x^3-3x^2-3x-1

=-6x^2-2

3: =1-3x+3x^2-x^3+x^3+9x^2+27x+27

=24x+12x^2+28

4: =x^3+6x^2y+12xy^2+8y^3-x^3+6x^2y-12xy^2+8y^3

=12x^2y+16y^3

5: =y^3-3y^2x+3yx^2-x^3-8x^3+12x^2y-6xy^2+y^3

=2y^3-9xy^2+15x^2y-9x^3

7: =8x^3-36x^2+54x-27-2x(4x^2+4x+1)

=8x^3-36x^2+54x-27-8x^3-8x^2-2x

=-44x^2+52x-27

8: =27x^3-27x^2+9x-1-27x^3-27x^2

=-54x^2+9x-1