Điều kiện: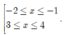 

Đặt t= x²- 2x; t’ = 2x- 2 và t’ =0 khi x= 1.

Bảng biến thiên 

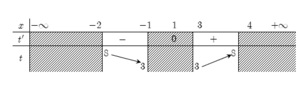
Dựa vào bảng biến thiên suy ra tập giá trị của t là [ 3; 8].

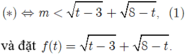
Để (* )  có nghiệm khi và chỉ khi ( 1)  có nghiệm 

Xét hàm số 

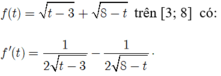
Cho f’ (t) =0 khi  nên 

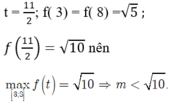
Vậy m ∈ (-∞; √10) sẽ thỏa mãn yêu cầu bài toán.

Chọn D.

Thay x =-3 vào vế trái của phương trình , ta có:

3. - 3 2 +2(-3) -21 =27 – 6 -21 =0

Vậy x = -3 là nghiệm của phương trình 3 x 2  +2x -21 =0

Theo hệ thức vi-ét ta có : x 1 x 2  = c/a = -21/3 = -7 ⇒  x 2  = -7/ x 1  = -7/-3 = 7/3

Vậy nghiệm còn lại là x = 7/3

Gửi ạ 

Lời giải:

1.

$4x+9=0$

$4x=-9$

$x=\frac{-9}{4}$
2.

$-5x+6=0$

$-5x=-6$

$x=\frac{6}{5}$

3.

$x^2-1=0$

$x^2=1=1^2=(-1)^2$

$x=\pm 1$

4.

$x^2-9=0$

$x^2=9=3^2=(-3)^2$

$x=\pm 3$

5.

$x^2-x=0$

$x(x-1)=0$

$x=0$ hoặc $x-1=0$

$x=0$ hoặc $x=1$

6.

$x^2-2x=0$

$x(x-2)=0$

$x=0$ hoặc $x-2=0$

$x=0$ hoặc $x=2$

7.

$x^2-3x=0$

$x(x-3)=0$

$x=0$ hoặc $x-3=0$ 

$x=0$ hoặc $x=3$

8.

$3x^2-4x=0$

$x(3x-4)=0$

$x=0$ hoặc $3x-4=0$

$x=0$ hoặc $x=\frac{4}{3}$

a: Khi x=3 thì pt sẽ là:

3^2-2*3+m+3=0

=>m-6+9+3=0

=>m+6=0

=>m=-6

x1+x2=2

=>x2=2-3=-1

b:

Δ=(-2)^2-4(m+3)

=4-4m-12

=-4m-8

Để phương trình có hai nghiệm phân biệt thì:

-4m-8>=0

=>m<=-2

x1^3+x2^3=8

=>(x1+x2)^3-3x1x2(x1+x2)=8

=>2^3-3*2(m+3)=8

=>6(m+3)=0

=>m+3=0

=>m=-3(nhận)

Để pt có 2 nghiệm trái dấu \(\Leftrightarrow ac< 0\Leftrightarrow4m+5< 0\Rightarrow m< -\dfrac{5}{4}\)

\(x_1=3\left|x_2\right|>0\Rightarrow x_1>0\Rightarrow x_2< 0\Rightarrow3\left|x_2\right|=-3x_2\)

\(\Rightarrow x_1=-3x_2\)

Kết hợp với hệ thức Viet ta được: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1=-3x_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1=3\\x_2=-1\end{matrix}\right.\)

Mà \(x_1x_2=4m+5\Rightarrow4m+5=-3\Rightarrow m=-2\)

Lời giải:

Để pt có 2 nghiệm $x_1,x_2$ thì:

$\Delta'=1+(m-1)(m-3)\geq 0\Leftrightarrow (m-2)^2\geq 0\Leftrightarrow m\in\mathbb{R}$

Ta có:

$x^2-2x-(m-1)(m-3)=0$

$\Leftrightarrow [x-(m-1)][x+(m-3)]=0$

$\Rightarrow (x_1,x_2)=(m-1,3-m)$ và hoán vị

Nếu $x_1=m-1; x_2=3-m$ thì: $A=(x_1+1)x_2=m(3-m)=3m-m^2=\frac{9}{4}-(m-\frac{3}{2})^2\leq \frac{9}{4}$

Vậy $A_{\max}=\frac{9}{4}$ khi $m=\frac{3}{2}$

Nếu $x_1=3-m; x_2=m-1$ thì:

$A=(4-m)(m-1)=5m-4-m^2=\frac{9}{4}-(m-\frac{5}{2})^2\leq \frac{9}{4}$

Vậy $A_{\max}=\frac{9}{4}$ khi $m=\frac{5}{2}$

Vậy tóm lại $m=\frac{3}{2}$ hoặc $m=\frac{5}{2}$ thì $A_{\max}$