Cho đa thức Q (x) =x2 - 2x +3
Tính Q (-1); Q(3); Q(1)
Cho các đa thức M(x)=-2x^3+4x+x^2-3 và N(x)= 2x^3+x2-5-4x 1) Tính P(x) = M(x) + N(x) 2) Tìm nghiệm của đa thức P(x) 3) Tìm đa thức Q(x) biết Q(x) + N(x) = M(x)
1: P(x)=M(x)+N(x)
=-2x^3+x^2+4x-3+2x^3+x^2-4x-5
=2x^2-8
2: P(x)=0
=>x^2-4=0
=>x=2 hoặc x=-2
3: Q(x)=M(x)-N(x)
=-2x^3+x^2+4x-3-2x^3-x^2+4x+5
=-4x^3+8x+2
Cho đa thức P ( x ) = x 3 - 4 x 2 + 3 - 2 x 3 + x 2 + 10 x - 1
Tìm đa thức Q(x) biết P ( x ) + Q ( x ) = x 3 + x 2 + 2 x - 1
A. - 4 x 2 - 8 x - 3
B. 2 x 3 - 4 x 2 + 8 x - 3
C. 2 x 3 + 4 x 2 - 8 x - 3
D. 4 x 2 - 8 x - 3
Chọn C
Ta có: P(x) + Q(x) = x3+ x2+ 2x-1
⇒ Q(x) = (x3 + x2 + 2x-1) - P(x)
= 2x3 + 4x2 - 8x - 3.
Bài 1 . cho hai đa thức: P(x) = 4x4 - 2x3 - 7x2 + 2x + 1/3 và Q(x) = x4 + 3x3 - 6x2 - x - 1/4
a. Tính P(x) + Q(x);
b. Tính P(x) - Q(x).
Bài 2. cho đa thức: M(x) = x2 - 2x3 + x + 5 và N(x) = 2x3 - x - 6
a. Tính M(2)
b. Tìm đa thức A(x) sao cho A(x) = M(x) + N(x); A(x), tính B(x) = M(x) - N(x)
c. Tìm nghiệm của đa thức A(x)
Bài 3. Tìm nghiệm của các đa thức sau:
a. 2x - 8 b. 2x + 7 c. 4 - x2 d. 4x2 - 9
e. 2x2 - 6 f. x(x - 1) g. x + 2x h. x( x + 2 )
Bài 4. cho hai đa thức: f(x) = 2x4 + 3x2 - x + 1 - x2 - x4 - 6x3
g(x) = 10x3 + 3 - x4 - 4x3 + 4x - 2x2
a. Thu gọn đa thức: f(x), g(x) và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.
b. Tính h(x) = f(x) + g(x); K(x) = f(x) - g(x)
c. Tìm nghiệm của đa thức h(x)
Bài 5. Tìm nghiệm của các đa thức:
a. 9 - 3x b. -3x + 4 c. x2 - 9 d. 9x2 - 4
e. x2 - 2 f. x( x - 2 ) g. x2 - 2x h. x(x2 + 1 )
Tách ra, dài quá mn đọc là mất hứng làm đó.
Bài 1: Cho hai đa thức P(x) = 5x3 – 3x + 7 – x;
Q(x) = –5x3 + 2x – 3 + 2x – x2 – 2.
a) Thu gọn hai đa thức P(x), Q(x) và xác định bậc của hai đa thức đó.
b) Tìm đa thức M(x) sao cho P(x) = M(x) – Q(x).
c) Tìm nghiệm của đa thức M(x).
`a,`
`P(x)=5x^3 - 3x + 7 - x`
`= 5x^3 +(-3x-x)+7`
`= 5x^3-4x+7`
Bậc: `3`
`Q(x)=-5x^3 + 2x - 3 + 2x - x^2 - 2`
`= -5x^3-x^2+(2x+2x)+(-3-2)`
`= -5x^3-x^2+4x-5`
Bậc: `3`
`b,`
`P(x)=M(x)-Q(x)`
`-> M(x)=P(x)+Q(x)`
`M(x)=(5x^3-4x+7)+(-5x^3-x^2+4x-5)`
`M(x)=5x^3-4x+7-5x^3-x^2+4x-5`
`M(x)=(5x^3-5x^3)-x^2+(-4x+4x)+(7-5)`
`M(x)=-x^2+2`
`c,`
`M(x)=-x^2+2=0`
`\leftrightarrow -x^2=0-2`
`\leftrightarrow -x^2=-2`
`\leftrightarrow x^2=2`
`\leftrightarrow `\(\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy, nghiệm của đa thức là \(x=\left\{\sqrt{2};-\sqrt{2}\right\}\)
Bài 1 Cho hai đa thức: P(x) = 4x3 – 3x + x2 + 7 + x
Q(x) =– 4x3 + 2x – 2 + 2x – x2 – 1
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến
b) Tính M(x) = P(x) + Q(x) và N(x) = P(x) – Q(x)
c) Tìm nghiệm của đa thức M(x)
a: \(P\left(x\right)=4x^3+x^2-2x+7\)
\(Q\left(x\right)=-4x^3-x^2+4x-3\)
b: \(M\left(x\right)=4x^3+x^2-2x+7-4x^3-x^2+4x-3=2x+4\)
\(N\left(x\right)=8x^3+2x^2-6x+10\)
c: Đặt M(x)=0
=>2x+4=0
hay x=-2
\(a,Q_{\left(x\right)}=-4x^3+2x-2+2x-x^2-1\\ Q_{\left(x\right)}=-4x^3-x^2+4x-3\\ P_{\left(x\right)}=4x^3-3x+x^2+7+x\\ P_{\left(x\right)}=4x^3+x^2-2x+7\)
\(b,M_{\left(x\right)}=P_{\left(x\right)}+Q_{\left(x\right)}\\ M_{\left(x\right)}=4x^3+x^2-2x+7-4x^3-x^2+4x-3\\ M_{\left(x\right)}=2x+4\)
\(N_{\left(x\right)}=4x^3+x^2-2x+7+4x^2+x^2-4x+3\\ N_{\left(x\right)}=8x^3+2x^2-6x+10\)
\(c,M_{\left(x\right)}=0\\ \Rightarrow2x+4=0\\ \Rightarrow2x=-4\\ \Rightarrow x=-2\)
a)\(P\left(x\right)=4x^3+x^2-2x+7\)
\(Q\left(x\right)=-4x^3-x^2+4x-3\)
b)\(M\left(x\right)=4x^3+x^2-2x+7-4x^3-x^2-4x+3\)
\(M\left(x\right)=-6x+10\)
\(N\left(x\right)=4x^3+x^2-2x+7+4x^3+x^2+4x-3\)
\(N\left(x\right)=8x^3+2x^2+2x+4\)
c) cho M(x) = 0
\(=>-6x+10=0\)
\(-6x=-10\Rightarrow x=-\dfrac{10}{-6}=\dfrac{5}{3}\)
Bài 1. (2,0 điểm) Cho hai đa thức P(x) = 5x3 – 3x + 7 – x;
Q(x) = –5x3 + 2x – 3 + 2x – x2 – 2.
a) Thu gọn hai đa thức P(x), Q(x) và xác định bậc của hai đa thức đó.
b) Tìm đa thức M(x) sao cho P(x) = M(x) – Q(x).
c) Tìm nghiệm của đa thức M(x).
a: \(P\left(x\right)=5x^3-4x+7\)
Bậc 3
\(Q\left(x\right)=-5x^3-x^2+4x-5\)
Bậc 3
b: M(x)=P(x)+Q(x)
=5x^3-4x+7-5x^3-x^2+4x-5=-x^2+2
c: M(x)=0
=>2-x^2=0
=>\(x=\pm\sqrt{2}\)
Bài 3: cho đa thức P(x)= 5x3 - x4 + 2x - x2 + x4 + 2x2 - 5x3 - 3
a, thu gọn tìm bậc của đa thức
b, Chứng tỏ X=-3 ; x=1 là các nghiệm của đa thức P(x)
c, Tìm nghiệm của đa thức Q(x) biết Q(x) + P(x) = x2 - x
Cần gấp
a. cậu thu gọn bằng cách dùng t/c kết hợp và giao hoán
b. cậu thay từng giá vào biểu thức vừa được rút gọn để tìm
c. thì.... tớ ko biết
Cho đa thức: Q(x) = 4x3 + 7x + 9 + x2 – 2x - 3
a) Thu gọn đa thức Q(x), cho biết hệ số tự do, hệ số cao nhất của đa thức Q(x)
b) Tính giá trị của đa thức Q(x) với x = 2. cần gấp
a)\(Q\left(x\right)=4x^3+x^2+\left(7x-2x\right)+\left(9-3\right)=4x^3+x^2+5x+6\)
hệ số tự do : 6
hệ số cáo nhất : 6
b) thay x = 2 vào Q(x) ta đa
\(Q\left(2\right)=4.2^3+2^2+5.2+6=4.8+4+10+6\)
\(Q\left(2\right)=32+4+10+6=52\)
`a)`
`Q(x)=4x^3+7x+9+x^2-2x-3`
`Q(x)=4x^3+x^2+(7x-2x)+(9-3)`
`Q(x)=4x^3+x^2+5x+6`
`@` Hệ số tự do: `6`
`@` Hệ số cao nhất: `4`
_______________________________________
`b)` Thay `x=2` vào `Q(x)`. Có:
`Q(x)=4.2^3+2^2+5.2+6`
`Q(x)=32+4+10+6=52`
a, \(Q = 4x^3 + x^2 + (7x-2x) + (9-3) = 4x^3 + x^2 + 5x + 6 = 4x^3 + (x+2)(x+3).\)
Hệ số tự do là $6$, hệ số cao nhất là $5$.
b,Giá trị của đa thức khi $x = 2$ là:
$Q = 42^3 + (2+2)(2+3) = 32 + 4 . 5 = 52.$
Vậy khi $x = 2$ thì giá trị đa thức trên là $52$.
Cho hai đa thức P(x)= x5-5x3+4x+1, Q(x)=2x2+x-1. Gọi x1,x2,x3,x4,x5 là các ng của P(x)
Tính Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)
Vì P(x) có hệ số bậc cao nhất là 1
Nên P(x) có thể được viết dưới dạng: \(P\left(x\right)=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\left(x-x_5\right)\)
Và \(P\left(-1\right)=\left(-1\right)^5-5\left(-1\right)^3+4\left(-1\right)+1=1\)
\(P\left(\frac{1}{2}\right)=\frac{77}{32}\)
Ta có: \(Q\left(x\right)=2x^2+x-1=2x^2+2x-x-1=2x\left(x+1\right)-\left(x+1\right)=\left(x+1\right)\left(2x-1\right)\)
=> \(Q\left(x_1\right).\text{}\text{}Q\left(x_2\right).\text{}\text{}Q\left(x_3\right).\text{}\text{}Q\left(x_4\right).\text{}\text{}Q\left(x_5\right)\text{}\text{}\)
\(=\left(x_1+1\right)\left(2x_1-1\right)\left(x_2+1\right)\left(2x_2-1\right)\left(x_3+1\right)\left(2x_3-1\right)\left(x_4+1\right)\left(2x_4-1\right)\left(x_5+1\right)\left(2x_5-1\right)\)
\(=32\left(-1-x_1\right)\left(\frac{1}{2}-x_1\right)\left(-1-x_2\right)\left(\frac{1}{2}-x_2\right)\left(-1-x_3\right)\left(\frac{1}{2}-x_3\right)\left(-1-x_4\right)\left(\frac{1}{2}-x_4\right)\left(-1-x_5\right)\left(\frac{1}{2}-x_5\right)\)\(=32.P\left(-1\right).P\left(\frac{1}{2}\right)=32.1.\frac{77}{32}=77\)
\(p\left(x\right)=x^5-5x^3+4x+1=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\left(x-x_5\right)\)
\(Q\left(x\right)=2\left(\frac{1}{2}-x\right)\left(-1-x\right)\)
Do đó \(Q\left(x_1\right)\cdot Q\left(x_2\right)\cdot Q\left(x_3\right)\cdot Q\left(x_4\right)\cdot Q\left(x_5\right)\)
\(=2^5\left[\left(\frac{1}{2}-x_1\right)\left(\frac{1}{2}-x_2\right)\left(\frac{1}{2}-x_3\right)\left(\frac{1}{2}-x_4\right)\left(\frac{1}{2}-x_5\right)\right]\)
\(=\left(-1-x_1\right)\left(-1-x_2\right)\left(-1-x_3\right)\left(-1-x_4\right)\left(-1-x_5\right)\)
\(=32P\left(\frac{1}{2}\right)\cdot\left[P\left(-1\right)\right]\)
\(=32\cdot\left(\frac{1}{32}-\frac{5}{8}+\frac{4}{2}+1\right)\left(-1+5-4+1\right)\)
\(=4300\)
*Mình không chắc*
Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức ?
a) P(x) = 2x + 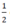 |
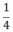 |
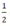 |
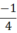 |
| b) Q(x) = x2 – 2x -3 | 3 | 1 | -1 |
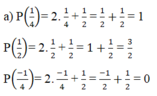
Vậy x = 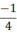 là nghiệm của đa thức P(x) = 2x +
là nghiệm của đa thức P(x) = 2x + 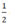
b) Q(3) = 32 – 2.3 – 3 = 9 – 6 – 3 = 0
Q(1) = 12 – 2.1 – 3 = 1 – 2 – 3 = - 4
Q(-1) = (-1)2 – 2.(-1) – 3 = 1 + 2 – 3 = 0
Vậy x = 3 và x = - 1 là nghiệm của đa thức Q(x) = x2 – 2x – 3