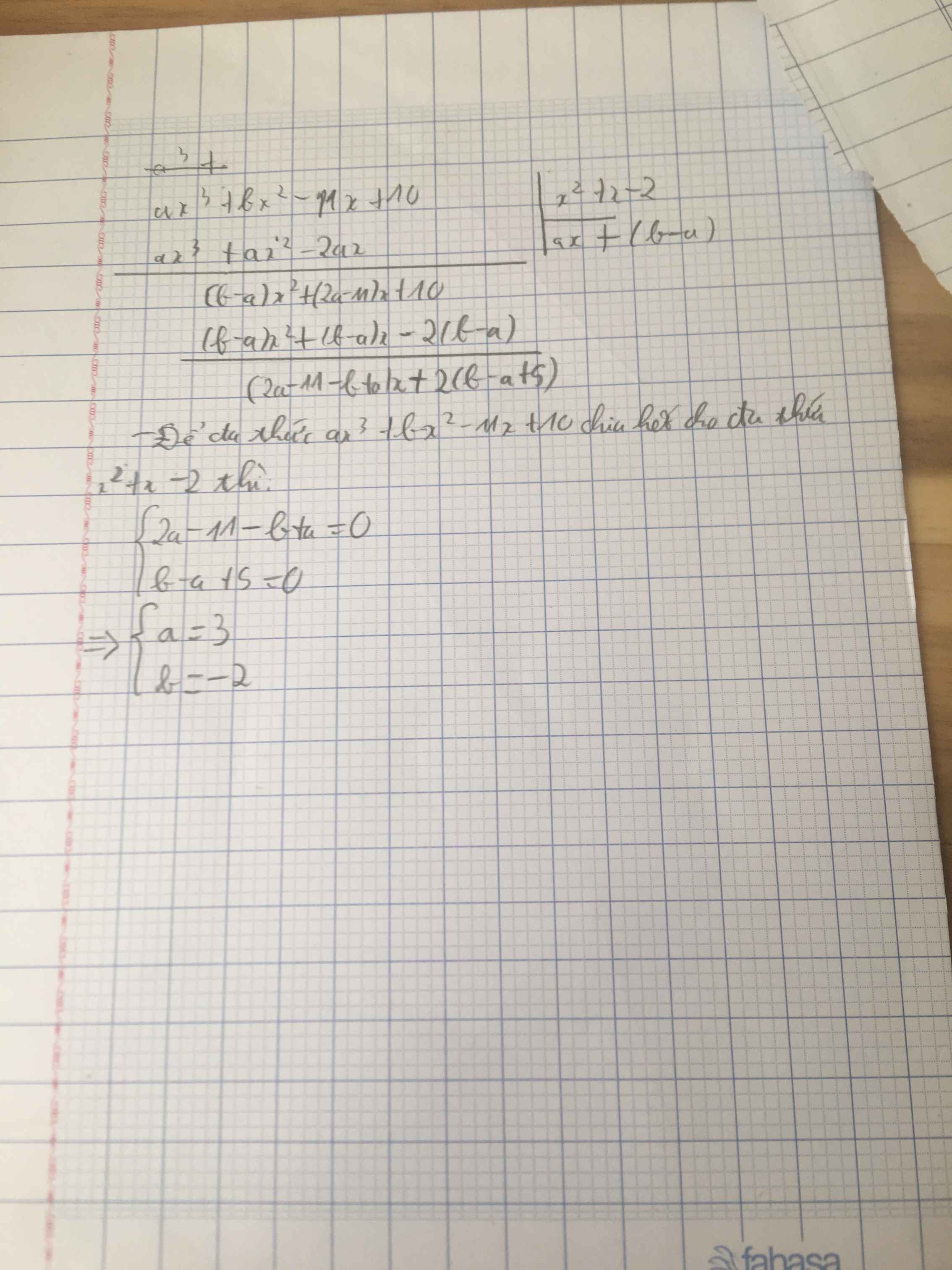\(\Leftrightarrow2x^3-3x^2+x+a=\left(x+3\right)\cdot a\left(x\right)\)

Thay \(x=-3\Leftrightarrow-54-27-3+a=0\Leftrightarrow a=84\)

Đa thức \(K\left(x\right)=6x^3-2x^2-ax-2\)chia hết cho nhị thức 2x - 3 khi \(\frac{3}{2}\)là nghiệm của K(x)

hay \(K\left(\frac{3}{2}\right)=0\Leftrightarrow6.\left(\frac{3}{2}\right)^3-2.\left(\frac{3}{2}\right)^2-\frac{3}{2}a-2=0\)

\(\Leftrightarrow\frac{81}{4}-\frac{9}{2}-\frac{3}{2}a-2=0\Leftrightarrow\frac{3}{2}a=\frac{55}{4}\)

\(\Leftrightarrow a=\frac{55}{6}\)

Vậy \(a=\frac{55}{6}\)thì \(6x^3-2x^2-ax-2\)chia hết cho  2x - 3

Vì \(x^{2017}-ax^{2016}+ax-1⋮\left(x-1\right)^2\Rightarrow x^{2017}-ax^{2016}+ax-1=\left(x-1\right)^2.Q\left(x\right)\text{đúng}\forall x\)

Thay x = 1 vào đẳng thức trên, ta có: 

1 - a + a - 1 = 0 (đúng) => Có vô số số hữu tỉ a thoả mãn để bài

\(6x^2-5x+a=\left(6x^2-5x-6\right)+a+6=\left(3x+2\right)\left(2x-3\right)+a+6\)

Do \(\left(3x+2\right)\left(2x-3\right)⋮3x+2\) nên đa thức đã cho chia hết 3x+2 khi và chỉ khi:

\(a+6=0\Rightarrow a=-6\)

Ta có

Để phép chia trên là phép chia hết thì R = a + 12 = 0 ó a = -12

Đáp án cần chọn là: C

(10 x 2 – 7x + a) ⁝ (2x – 3)

Để 10 x 2 – 7x + a chia hết cho 2x – 3 thì a + 12 = 0 ó a = -12

Đáp án cần chọn là: C

ơ sao lại bôi nhọ chữ thế bạn

\(x^3-3x+a⋮\left(x-1\right)^2\\ \Leftrightarrow x^3-3x+a=\left(x-1\right)^2\cdot A\left(x\right)\)

Thay \(x=1\), ta được:

\(1^3-3\cdot1+a=0\\ \Leftrightarrow a=2\)

Vậy \(a=2\) thì thỏa mãn đề 

Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$

$x^2+x-2=(x-1)(x+2)$

Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$

$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức) 

$\Leftrightarrow a+b-1=-8a+4b+32=0$

$\Leftrightarrow a=3; b=-2$ 

Câu hỏi của Phạm Thị Quỳnh Tú - Toán lớp 8 - Học toán với OnlineMath

Tham khảo

gọi f(x)=x^3+5x^2-6x+a

g(x)=x-2

ta có

f(x)=x^3+5x^2-6x+a

f(2)=2^3+5*2^2-6*2+a

f(2)=16+a

áp dụng hệ quả bơzu ta có

16+a=0 <=> a=-16

vậy ...

x³ + 5x² - 6x + a \(⋮\) x-2

Đặt  F(x) = x³ +5x² - 6x + a 

theo Bezout ta có : F(x) \(⋮\) x - 2 

\(\Leftrightarrow\) F(2) = 0 \(\Leftrightarrow\) 2³ + 5.2² -6.2 + a = 0

\(\Leftrightarrow\) 8 + 20 - 12 + a = 0

\(\Leftrightarrow\) 16 + a = 0

\(\Leftrightarrow\) a = -16

Kết luận với a = -16 thì x³ + 5x² - 6x + a \(⋮\) x -2