có giá trị của x hay không khi
\(x^2-x^2=x^2\left(x\ne0\right)\)
Cho đơn thức: \(A=\left(2a^2+\dfrac{1}{a^2}\right)x^2y^4z^6\left(a\ne0\right)\). Chọn câu đúng nhất:
A. Giá trị của A luôn không âm với mọi x, y
B. Nếu A = 0 thì x = y = z = 0
C. Chỉ có một giá trị của x để A = 0
D. Chỉ có một giá trị của y để A = 0
Một phân thức có giá trị bằng 0 khi giá trị của tử thức bằng 0 còn giá trị của mẫu thức khác 0. Ví dụ giá trị của phân thức \(\dfrac{x^2-25}{x+1}=0\) khi \(x^2-25=0\) và \(x+1\ne0\) hay \(\left(x-5\right)\left(x+5\right)=0\) và \(x\ne-1\)
Vậy giá trị của phân thức này bằng 0 khi \(x=\pm5\)
Tìm các giá trị của x để giá trị của mỗi phân thức sau bằng 0 :
a) \(\dfrac{98x^2-2}{x-2}\)
b) \(\dfrac{3x-2}{x^2+2x+1}\)
a, Ta có : \(\dfrac{98x^2-2}{x-2}=0\Leftrightarrow\left\{{}\begin{matrix}98x^2-2=0\\x-2\ne0\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x^2=\dfrac{1}{49}\\x\ne2\end{matrix}\right.\Leftrightarrow x=\pm\dfrac{1}{7}\)
Vậy giá trị của phân thức này bằng 0 khi \(x=\pm\dfrac{1}{7}\)
b, Ta có : \(\dfrac{3x-2}{x^2+2x+1}=0\Leftrightarrow\dfrac{3x-2}{\left(x+1\right)^2}=0\Leftrightarrow\left\{{}\begin{matrix}3x-2=0\\\left(x+1\right)^2\ne0\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\x\ne-1\end{matrix}\right.\)
Vậy giá trị của phân thức này bằng 0 khi \(x=\dfrac{2}{3}\)
a)
98x^2 -2 =0 =>x^2 =1/49 => x= -+1/7 nhận
b)
3x-2=0=>x=2/3 nhận
1.tìm m để phương trình \(x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(x\ne0\right)\) có nghiệm
2. cho hàm số y=f(x)=\(x^2-4x+3\)
tìmcác giá trị nguyên của m để
\(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\) có 6 nghiệm phân biệt
\(1.x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(1\right)\)\(đặt:x^2+\dfrac{1}{x^2}=t\)
\(x>0\Rightarrow t\ge2\sqrt{x^2.\dfrac{1}{x^2}}=2\)
\(x< 0\Rightarrow-t=-x^2+\dfrac{1}{\left(-x^2\right)}\ge2\Rightarrow t\le-2\)
\(\Rightarrow t\in(-\infty;-2]\cup[2;+\infty)\left(2\right)\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-2mt+2m-1=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-2m+1\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\notin\left(2\right)\\t=2m-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2m-1\le-2\\2m-1\ge2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{3}{4}\end{matrix}\right.\)
\(2.\) \(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=3-m\end{matrix}\right.\)
\(dựa\) \(vào\) \(đồ\) \(thị\) \(f\left(\left|x\right|\right)\) \(\Rightarrow f\left(\left|x\right|\right)=-1\) \(có\) \(2nghiem\) \(pb\)
\(\left(1\right)có\) \(6\) \(ngo\) \(pb\Leftrightarrow\left\{{}\begin{matrix}-1< 3-m< 3\\3-m\ne-1\\\end{matrix}\right.\)\(\Leftrightarrow0< m< 4\)
\(\Rightarrow m=\left\{1;2;3\right\}\)
Chứng minh rằng :
a) Giá trị của biểu thức : \(\left(\frac{x+2}{x}\right)^2:\left(\frac{x^2+4}{x^2}+\frac{4}{x+1}\left(\frac{1}{x}+1\right)\right)\)bằng 1 với mọi giá trị \(x\ne0;x\ne-2\)
b) Giá trị của biểu thức\(\left(\frac{x}{2x-6}-\frac{x^2}{x^2-9}+\frac{x}{2x-9}\left(\frac{3}{x}-\frac{1}{x-3}\right)\right):\frac{x^2-5x-6}{18-2x^2}\) bằng 1 với mọi giá trị \(x\ne0;x\ne+-3;x\ne-1;x\ne6\)
a)\(\frac{x^2+4}{x^2}+\frac{4}{x+1}\left(\frac{1}{x}+1\right)\)
\(=\frac{x^2+4}{x^2}+\frac{4}{x+1}.\frac{x+1}{x}\)
\(=\frac{x^2+4}{x^2}+\frac{4}{x}\)
\(=\frac{x^2+4x+4}{x^2}\)
\(\left(\frac{x+2}{x}\right)^2\)
=>phép chia = 1 với mọi x # 0 và x#-1
b)Cm tương tự
Ta thấy A gồm có 99 số hạng nên ta nhóm mỗi nhóm 3 số hạng.
Ta có: A = 1 + 5 + 52 + 53 + 54 + 55 +...+ 597 + 598 + 599
= (1 + 5 + 52 )+ (53 + 54 + 55 )+...+( 597 + 598 + 599 )
=(1 + 5 + 52 )+ 53(1 + 5 + 52 ) +...+ 597(1 + 5 + 52 )
= ( 1 + 5 + 52)(1 + 53+....+597)
= 31(1 + 53+....+597)
Vì có một thừa số là 31 nên A chia hết cho 31.
P/s Đừng để ý câu trả lời của mình
Chứng minh rằng :
a) Giá trị của biểu thức :
\(\left(\dfrac{x+1}{x}\right)^2:\left[\dfrac{x^2+1}{x^2}+\dfrac{2}{x+1}\left(\dfrac{1}{x}+1\right)\right]\) bằng 1 với mọi giá trị \(x\ne0;x\ne-1\)
b) Giá trị của biểu thức :
\(\dfrac{x}{x-3}-\dfrac{x^2+3x}{2x+3}\left(\dfrac{x+3}{x^2-3x}-\dfrac{x}{x^2-9}\right)\) bằng 1 khi \(x\ne0;x\ne-3;x\ne3;x\ne-\dfrac{3}{2}\)
Quan sát đồ thị của hàm số \(y=f\left(x\right)=-x^2\) trên \(R\) (H.6.5).
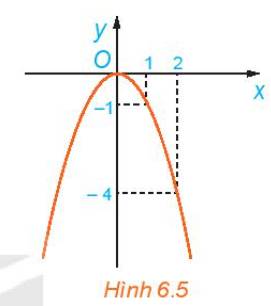
Hỏi:
a) Giá trị của \(f\left(x\right)\) tăng hay giảm khi x tăng trên khoảng \(\left(-\infty;0\right)\)?
b) Giá trị của \(f\left(x\right)\) tăng hay giảm khi x tăng trên khoảng \(\left(0;+\infty\right)\)?
Dựa vào đồ thị, ta thấy:
a) Trên khoảng \(\left( { - \infty ;0} \right)\) , giá trị của f(x) tăng
b) Trên khoảng \(\left( {0; + \infty } \right)\) , giá trị của f(x) giảm
Cho đa thức \(f\left(x\right)=ax^2+bx+c\) \(\left(a\ne0\right)\). Tìm a, b, c biết \(f\left(x\right)-2020\)chia hết cho x - 1, \(f\left(x\right)+2021\) chia hết cho x + 1 và \(f\left(x\right)\) nhận giá trị bằng 2 khi x = 0
Mình có nghĩ ra cách này mọi người xem giúp mình với
f(x) = \(ax^2+bx+c\)
Ta có f(0) = 2 => c = 2
Ta đặt Q(x) = \(ax^2+bx+c-2020\)
và G(x) = \(ax^2+bx+c+2021\)
f(x) - 2020 chia cho x - 1 hay Q(x) chia cho x - 1 được số dư
\(R_1\) = Q(1) = \(a.1^2+b.1+c-2020=a+b+c-2020\)
Mà Q(x) chia hết cho x-1 nên \(R_1\) = 0
hay \(a+b+c-2020=0\). Mà c = 2 => a + b = 2018 (1)
G(x) chia cho x + 1 số dư
\(R_2\) = G(-1) = \(a.\left(-1\right)^2+b.\left(-1\right)+c+2021=a-b+2+2021\)
Mà G(x) chia hết cho x + 1 nên \(R_2\)=0
hay \(a-b+2+2021=0\) => \(a-b=-2023\) (2)
Từ (1) và (2) suy ra: \(\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=-\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)
\(f\left(0\right)=2\Rightarrow c=2\)
\(f\left(x\right)-2020\) chia hết \(x-1\Rightarrow f\left(1\right)-2020=0\)
\(\Rightarrow a+b+c-2020=0\Rightarrow a+b-2018=0\)
\(f\left(x\right)+2021\) chia hết \(x+1\Rightarrow f\left(-1\right)+2021=0\)
\(\Rightarrow a-b+c+2021=0\Rightarrow a-b+2023=0\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)
Với \(x\ne0\)và \(y\ne0\)Chứng minh rằng
\(\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2+\left(xy+\frac{1}{xy}\right)^2-\left(x+\frac{1}{x}\right)\left(y+\frac{1}{y}\right)\left(xy+\frac{1}{xy}\right)\)không phụ thuộc vào giá trị của x và y
\(\left(xy+\frac{1}{xy}\right)^2-\left(x+\frac{1}{x}\right)\left(y+\frac{1}{y}\right)\left(xy+\frac{1}{xy}\right)\)
\(=\left(xy+\frac{1}{xy}\right)\left[\left(xy+\frac{1}{xy}\right)-\left(x+\frac{1}{x}\right)\left(y+\frac{1}{y}\right)\right]\)
\(=\left(xy+\frac{1}{xy}\right)\left(xy+\frac{1}{xy}-xy-\frac{x}{y}-\frac{y}{x}-\frac{1}{xy}\right)\)
\(=\left(xy+\frac{1}{xy}\right)\left(-\frac{x}{y}-\frac{y}{x}\right)\)
\(=-\left(xy+\frac{1}{xy}\right)\left(\frac{x}{y}+\frac{y}{x}\right)=-\left(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}\right)\)
\(-\left(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}\right)+\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2\)
\(=4\)
Vậy giá trị bt ko phụ thuộc vào biến
bn có thể giải thích rõ hơn tại sao lại bằng 4 được không? Dù gì thì cx cảm ơn bn đã tl câu hỏi của mk
Cho 3x-y=3z và 2x+y=7z. Tính giá trị của biểu thức: \(M=\dfrac{x^2-2xy}{x^2+y^2}\left(x\ne0,y\ne0\right)\)
Ta có: \(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Leftrightarrow3x-y+2x+y=10z\)
\(\Leftrightarrow5x=10z\)
hay x=2z
Thay x=2z vào biểu thức 3x-y=3z, ta được:
\(3\cdot2z-y=3z\)
\(\Leftrightarrow6z-y=3z\)
hay y=3z
Thay x=2z và y=3z vào biểu thức \(M=\dfrac{x^2-2xy}{x^2+y^2}\), ta được:
\(M=\dfrac{\left(2z\right)^2-2\cdot2z\cdot3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{13z^2}=\dfrac{-8z^2}{13z^2}=\dfrac{-8}{13}\)
Vậy: \(M=\dfrac{-8}{13}\)
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)