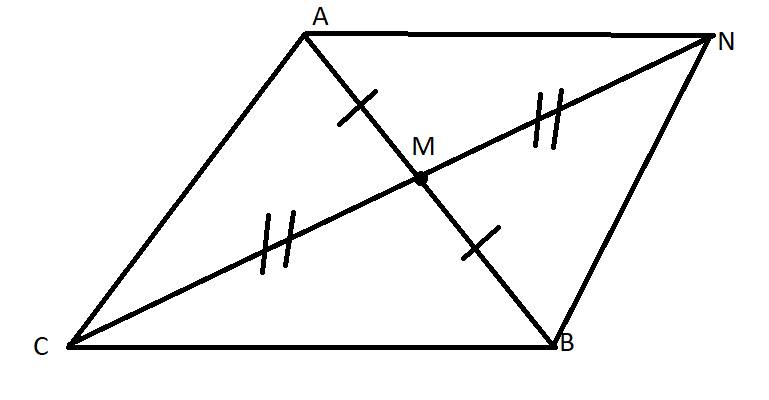
a, Xét ΔAMN và ΔBMC:

AM=BM(M là trung điểm của AB)

MC=MN(GT)

\(\widehat{AMN}=\widehat{BMC}\) (hai góc đối đỉnh)

=>ΔAMN=ΔBMC(c.g.c)

b, ΔAMN=ΔBMC=>\(\widehat{ANM}=\widehat{MCB}\) (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong

=>AN//BC

c,+) ΔAMN=ΔBMC =>AN=BC(cạnh tương ứng)

+)Xét ΔAMC và ΔNMB

AM=BM(M là trung điểm của AB)

MC=MN(GT)

\(\widehat{AMC}=\widehat{NMB}\)

=>ΔAMC=ΔNMB(c.g.c)=>AC=BN(cạnh tương ứng)

+)Xét ΔNAC và ΔCBN

AC=BN(CMT)

AN=BC(CMT)

CN là cạnh chung

=>ΔNAC=ΔCBN(c.c.c)

a: Xét ΔAMN và ΔBMC có 

MA=MB

\(\widehat{AMN}=\widehat{BMC}\)

MN=MC

Do đó: ΔAMN=ΔBMC

b: Xét tứ giác ACBN có

M là trung điểm của AB

M là trung điểm của CN

Do đó: ACBN là hình bình hành

SUy ra: NB//AC

a)       Xét \(\Delta BACvà\Delta NAMcó\)

                 \(\widehat{BAC}=\widehat{NAM}\) ( đối đỉnh )

                 \(BA=NA\) ( gt )

                  \(CA=MA\) ( gt )

\(\Rightarrow\Delta BAC=\Delta NAM\) ( c.g.c )

\(\Rightarrow BC=MN\) ( 2 cạnh tương ứng )

mik chỉ lm đc v hoi xin lũi bn _{do chx hiểu cái ý 2 câu a}

a) Xét Δ AMN và Δ BMC có:

+ MN = MC (gt).

+ \(\widehat{AMN} = \widehat{BMC}\) (2 góc đối đỉnh).

+ MA + MB (M là trung điểm của AB).

\(\Rightarrow\) Δ AMN = Δ BMC (c - g - c).

\(\Rightarrow\) \(\widehat{MAN} = \widehat{MBC}\) (2 góc tương ứng).

Mà 2 góc này ở vị trí so le trong.

\(\Rightarrow\) AN // BC (dhnb).

b) Xét tam giác ABC có:

+ M là trung điểm của AB (gt).

+ E là trung điểm của AC (gt).

\(\Rightarrow\) ME là đường trung bình.

\(\Rightarrow\) ME // BC và ME = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (1)

Xét tam giác NBA có:

+ M là trung điểm của AB (gt).

+ F là trung điểm của BN (gt).

\(\Rightarrow\) MF là đường trung bình.

\(\Rightarrow\) MF // BC và MF = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (2) 

Từ (1) và (2) \(\Rightarrow\) 3 điểm E, M, F thẳng hàng và MF = ME (cùng = \(\dfrac{1}{2}\) BC).

\(\Rightarrow\) M là trung điểm của EF (đpcm).

a: Xét ΔABM và ΔACM có 

AB=AC

AM chung

BM=CM

Do đó: ΔABM=ΔACM

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: Xét tứ giác AKBC có

N là trung điểm của AB

N là trung điểm của KC

Do đó: AKBC là hình bình hành

Suy ra: AK=BC=2MC

a: Xét tứ giác ACBN có

M là trung điểm chung của AB và CN

nên ACBN là hình bình hành

=>NB//AC và NB=AC

b: Xét tứ giác ABFC có

FB//AC
FB=AC

=>ABFC là hình bình hành

=>AF cắt BC tại trung điểm của mỗi đường

=>A,E,F thẳng hàng

a: Xét tứ giác ADCB có 

N là trung điểm của AC

N là trung điểm của DB

Do đó: ADCB là hình bình hành

Suy ra: DA=BC

a: Xét ΔMBC và ΔMAN có 

MB=MA

\(\widehat{BMC}=\widehat{AMN}\)

MC=MN

Do đó: ΔMBC=ΔMAN

Xét tứ giác ADBC có

M la trung điểm chung của AB và DC

nên ADBC là hình bình hành

=>góc ADB=góc ACB

Xét ΔABC có

MN//BC

AM/AB=1/2

=>N là trung điểm của AC

Xét ΔNBC và ΔNEA có

góc NCB=góc NAE

NC=NA

góc BNC=góc ENA

=>ΔNBC=ΔNEA

=>NB=NE

=>AECB là hình bình hành

=>CE=AB=AC=BD và góc AEC=góc ABC

=>góc AEC=góc ADB

Gọi giao của BD và CE là K

Xét ΔKDE có góc KDE=góc KED

nên ΔKDE cân tại K

=>KD=KE

=>KB=KC

=>K nằm trên trung trực của BC

mà AH là trung trực của BC

nên A,H,K thẳng hàng