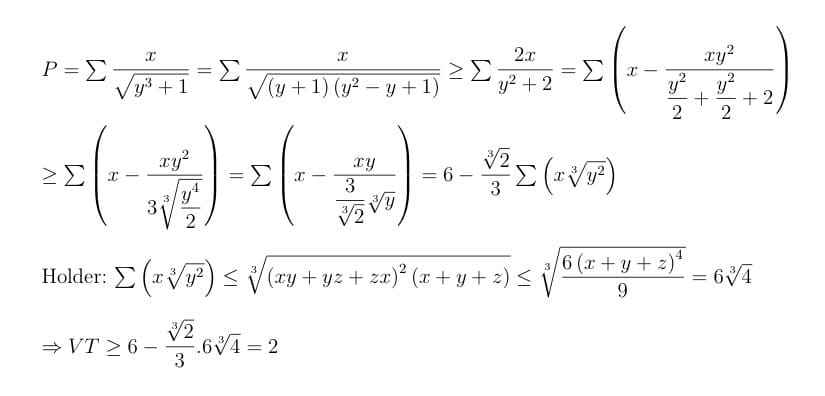1: Ta có: \(A=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)

\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

Để \(A=-\dfrac{1}{\sqrt{x}}\) thì \(x+\sqrt{x}=-\sqrt{x}+3\)

\(\Leftrightarrow x+2\sqrt{x}-3=0\)

\(\Leftrightarrow\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)=0\)

\(\Leftrightarrow x=1\left(nhận\right)\)

2: Để A nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)

\(\Leftrightarrow\sqrt{x}-3\in\left\{-1;1;2;-2;4;-4\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{2;4;5;1;7\right\}\)

\(\Leftrightarrow x\in\left\{16;25;1;49\right\}\)

1. 1/x + 2/1-x = (1/x - 1) + (2/1-x - 2) + 3

= 1-x/x + (2-2(1-x))/1-x  + 3

= 1-x/x + 2x/1-x + 3    >= 2√2 + 3

Dấu "=" xảy ra khi x =√2 - 1

2. a = √z-1, b = √x-2, c = √y-3 (a,b,c >=0)

=> P = √z-1 / z + √x-2 / x + √y-3 / y 

= a/a^2+1 + b/b^2+2 + c/c^2+3

a^2+1 >= 2a              => a/a^2+1 <= 1/2

b^2+2 >= 2√2 b          => b/b^2+2 <= 1/2√2

c^2+3 >= 2√3 c            => c/c^2+3 <= 1/2√3

=> P <= 1/2 + 1/2√2 + 1/2√3

Dấu = xảy ra khi a^2 = 1, b^2 = 2, c^2 =3

<=> z-1 = 1, x-2 = 2, y-3 = 3

<=> x=4, y=6, z=2

Dễ dàng nhận ra \(A\ge0\)

\(A^2=x+3-x+2\sqrt{x\left(3-x\right)}=3+2\sqrt{x\left(3-x\right)}\ge3\)

\(\Rightarrow A\ge\sqrt{3}\)

\(A_{min}=\sqrt{3}\) khi \(\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

Ta có: x \(\ge\) 0 \(\Rightarrow\) \(\sqrt{x}\ge0\)  (1)

Ta có: x \(\le\) 3 \(\Rightarrow\) 3 - x \(\ge\) 0 \(\Rightarrow\) \(\sqrt{3-x}\ge0\)  (2)

Từ (1) và (2) \(\Rightarrow\) \(\sqrt{x}+\sqrt{3-x}\ge0\)

Dấu "=" xảy ra \(\Leftrightarrow\) x = 0 hoặc x = 3

Chúc bn học tốt!

2. Xem tại đây

1.  \(P=\frac{1}{\sqrt{x.1}}+\frac{1}{\sqrt{y.1}}+\frac{1}{\sqrt{z.1}}\)

\(\ge\frac{1}{\frac{x+1}{2}}+\frac{1}{\frac{y+1}{2}}+\frac{1}{\frac{z+1}{2}}\)

\(=\frac{2}{x+1}+\frac{2}{y+1}+\frac{2}{z+1}\ge\frac{2.\left(1+1+1\right)^2}{x+y+z+3}=\frac{18}{3+3}=3\)

Đẳng thức xảy ra  \(\Leftrightarrow x=y=z=1\)

1 ) có cách theo cosi đó 

áp dụng cosi cho 3 số dương ta có \(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{x}}+x\ge3\sqrt[3]{\frac{1}{\sqrt{x}}\times\frac{1}{\sqrt{x}}\times x}=3\sqrt[3]{1}=3\)(1)

\(\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{y}}+y\ge3\)(2)

\(\frac{1}{\sqrt{z}}+\frac{1}{\sqrt{z}}+z\ge3\)(3)

cộng các vế của (1),(2),(3), đc \(2\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}\right)+\left(x+y+z\right)\ge9\Rightarrow2P+3\ge9\Rightarrow P\ge3\)

minP=3 khi x=y=z=1

Nãy mk nhầm thành Max, sorry :v

Ta có: x \(\ge\) 0 \(\Rightarrow\) \(\sqrt{x}\ge0\) (1)

x \(\le\) 3 \(\Rightarrow\) 3 - x \(\ge\) 0 \(\Rightarrow\) \(\sqrt{3-x}\ge0\) (2)

Từ (1) và (2) \(\Rightarrow\) \(\sqrt{x}.\sqrt{3-x}\ge0\)

Dấu "=" xảy ra \(\Leftrightarrow\) x = 0 hoặc x = 3

Chúc bn học tốt!

Với 0 \(\le\) x \(\le\) 3 ta có: A = \(\sqrt{x}\cdot\sqrt{3-x}\) = \(\sqrt{x\left(3-x\right)}\)

Áp dụng BĐT Cô-si cho 2 số x và 3 - x không âm ta được:

\(\dfrac{x+\left(3-x\right)}{2}\ge\sqrt{x\left(3-x\right)}\)

\(\Leftrightarrow\) \(\sqrt{x\left(3-x\right)}\le\dfrac{3}{2}\)

Hay A \(\le\) \(\dfrac{3}{2}\)

Dấu "=" xảy ra \(\Leftrightarrow\) x = 3 - x \(\Leftrightarrow\) x = \(\dfrac{3}{2}\)

Chúc bn học tốt!

Lời giải:

Do $x+y=1$ nên:

$P=\frac{x}{\sqrt{x+y-x}}+\frac{y}{\sqrt{x+y-y}}=\frac{x}{\sqrt{y}}+\frac{y}{\sqrt{x}}$
$=\frac{x^2}{x\sqrt{y}}+\frac{y^2}{y\sqrt{x}}$

$\geq \frac{(x+y)^2}{x\sqrt{y}+y\sqrt{x}}=\frac{1}{x\sqrt{y}+y\sqrt{x}}$ (áp dụng BĐT Cauchy-Schwarz)

Áp dụng BĐT Bunhiacopxky:

$(x\sqrt{y}+y\sqrt{x})^2\leq (x+y)(xy+xy)=2xy(x+y)\leq \frac{(x+y)^2}{2}(x+y)=\frac{1}{2}$

$\Rightarrow x\sqrt{y}+y\sqrt{x}\leq \frac{\sqrt{2}}{2}$

$\Rightarrow P\geq \frac{1}{x\sqrt{y}+y\sqrt{x}}\geq \frac{1}{\frac{\sqrt{2}}{2}}=\sqrt{2}$

Vậy $P_{\min}=\sqrt{2}$. Giá trị này đạt tại $x=y=\frac{1}{2}$.

Lời giải:
a. \(B=\frac{3(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}-\frac{\sqrt{x}+5}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{3(\sqrt{x}+1)-(\sqrt{x}+5)}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{2(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{2}{\sqrt{x}+1}\)

b.

\(P=2AB+\sqrt{x}=2.\frac{\sqrt{x}+1}{\sqrt{x}+2}.\frac{2}{\sqrt{x}+1}+\sqrt{x}=\frac{4}{\sqrt{x}+2}+\sqrt{x}\)

Áp dụng BĐT Cô-si:

$P=\frac{4}{\sqrt{x}+2}+(\sqrt{x}+2)-2\geq 2\sqrt{4}-2=2$

Vậy $P_{\min}=2$ khi $\sqrt{x}+2=2\Leftrightarrow x=0$