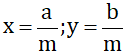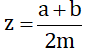Giả sử \(x,y,z\in Q,x=\frac{a}{b},b>0,y=\frac{c}{d},d>0,z=\frac{h}{g},g>0.\)

a) Nếu \(x=y\), tức là \(\frac{a}{b}=\frac{c}{d}\), thì ta suy ra \(\frac{a.d.g}{b.d.g}=\frac{b.c.g}{b.d.g}\left(1\right)\)

Xét \(x+z=\frac{a}{b}+\frac{h}{g}=\frac{a.d.g}{b.d.g}+\frac{b.d.h}{b.d.g}\left(2\right)\)

Thay kết quả \(\left(1\right)\) vào vế phải của \(\left(2\right)\) ta được:

\(x+z=\frac{b.c.g}{b.d.g}+\frac{b.d.h}{b.d.g}=\frac{c}{d}+\frac{h}{g}\Rightarrow x+z=y+z\)

b) Ngược lại, nếu \(x+z=y+z,\) tức là \(\frac{a}{b}+\frac{h}{g}=\frac{c}{d}+\frac{h}{g},\) thì ta suy ra

\(\frac{a.d.g}{b.d.g}+\frac{b.d.h}{b.d.g}=\frac{b.c.g}{b.d.g}+\frac{b.d.h}{b.d.g}\)

\(\Rightarrow\frac{a.d.g+b.d.h}{b.d.g}=\frac{b.c.g+b.d.h}{b.d.g}\)

\(\Rightarrow a.d.g+b.d.h=b.c.g+b.d.h\left(3\right)\)

Theo luật đơn giản ước của phép cộng các số nguyên, từ đẳng thức \(\left(3\right)\) ta có: \(a.d.g=b.c.g\). Do đó:

\(\frac{a.d.g}{b.d.g}=\frac{b.c.g}{b.d.g}\)

Suy ra \(\frac{a}{b}=\frac{c}{d}\)

Ta có :

(+) \(x=y\)

\(\Rightarrow\begin{cases}x+z=x+z\\y+z=x+z\end{cases}\)

=> x+z=y+z

(+) x+z=y+z

\(\Rightarrow x+z-z=y+z-z\)

=> x = y

Thanks nhưng còn cả mấy chục bài tại cô giao nhiều quá hai chú giúp nhé

C

vì x,y là các số dương =>x,y>0

ta có x>y(gt)=>x^2>xy

mà xy >y^2 ( vì x>y) =>x^2>y^2

vì x,y >0 và x^2>y^2 =>căn x^2 > căn y^2 => x>y (đpcm)

Thanks nhé!!

Vì 1 số bất kì nhân với 0 thì đều bằng 0 

nên \(x\times y=0\Rightarrow\orbr{\begin{cases}x=0\\y=0\end{cases}}\)

\(\left(2a-3\right)\times\left(\frac{3}{4}a+1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}2a-3=0\\\frac{3}{4}a+1=0\end{cases}\Rightarrow\orbr{\begin{cases}a=1,5\\a=-\frac{4}{3}\end{cases}}}\)

a.

- Áp dụng quy tắc chuyển vế ta có:

\(x-y>0\)

\(\Leftrightarrow x>0+y\)

\(\Leftrightarrow x>y\) (đpcm)

b.

- Áp dụng quy tắc chuyển vế, ta có:

\(x>y\)

\(\Leftrightarrow x-y>0\) (đpcm)

p/s: theo mình mấy cái này chuyển vế là ra mà cần j cm đâu :v mà thoi làm như n cho dễ

a) Nếu x - y > 0 <=> x - y + y > 0 + y <=> x > y

b) Nếu x > y <=> x - y > y - y <=> x - y > 0

Đề bài sai

Ví dụ: với \(a=1;b=2;c=3,d=4\) thì \(x=\dfrac{1}{2}\) ; \(y=\dfrac{3}{4}\) ; \(z=\dfrac{2}{3}\)

Khi đó  \(x< y\) nhưng \(z< y\)

\(\text{Vì }\dfrac{a}{b}< \dfrac{c}{d}\text{ nên }ad< bc\left(1\right)\)

\(\text{Xét tích}:a\left(b+d\right)=ab+ad\left(2\right)\)

                \(b\left(a+c\right)=ba+bc\left(3\right)\)

\(\text{Từ(1);(2);(3)}\Rightarrow a\left(b+d\right)< b\left(a+c\right)\text{ do đó }\dfrac{a}{b}< \dfrac{a+c}{b+d}\left(4\right)\)

\(\text{Tương tự ta có:}\dfrac{a+c}{b+d}< \dfrac{c}{d}\left(5\right)\)

\(\text{Từ (4);(5) ta được }\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\)

\(\Rightarrow x< y< z\)

Điều kiện \(\hept{\begin{cases}x\ge0\\y\ge0\end{cases}}\)

\(1+\sqrt{x+y+3}=\sqrt{x}+\sqrt{y}\)

\(\Leftrightarrow\sqrt{x+y+3}=\sqrt{x}+\sqrt{y}-1\)  (\(\sqrt{x}+\sqrt{y}-1>0\))

\(\Leftrightarrow\sqrt{x}+\sqrt{y}-\sqrt{xy}+1=0\)

\(\Leftrightarrow\sqrt{x}+\sqrt{y}=\sqrt{xy}-1\) (\(\sqrt{xy}-1>0\))

\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2=\left(\sqrt{xy}-1\right)^2\)

\(\Leftrightarrow4\sqrt{xy}=x+y-xy-1\)

Vì x, y nguyên nên \(\sqrt{xy}\) cũng phải nguyên

\(\Rightarrow\sqrt{x}+\sqrt{y}=\sqrt{xy}-1\) nguyên  (1)

Ta lại có: 

\(x-y=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)\)

\(\Rightarrow\sqrt{x}-\sqrt{y}\) nguyên (2)

Lấy (1) + (2) và  (1) - (2) ta có:

\(\hept{\begin{cases}\sqrt{x}+\sqrt{y}+\sqrt{x}-\sqrt{y}=2\sqrt{x}\\\sqrt{x}+\sqrt{y}-\sqrt{x}+\sqrt{y}=2\sqrt{y}\end{cases}}\)

\(\Rightarrow\sqrt{x},\sqrt{y}\) là số nguyên

Vậy x, y là bình phương đúng của 1 số nguyên.

mình sửa lại cái đề là: x, y nguyên nha m.n

Thật ra là có thể tìm được luôn là: \(\left(x,y\right)=\left(4,9;9,4\right)\)luôn đấy. 

đề khó hiểu vậy