Bài 1: Tập hợp Q các số hữu tỉ
Các câu hỏi tương tự
Câu Hỏi YESTERDAY AND TODAYDễ : So sánh các số hữu tỉ Khó : Giả sử (a, b, m ∈ Z; m 0) và x y. Hãy chứng minh nếu chọn thì ta có x z y
Đọc tiếp
Câu Hỏi YESTERDAY AND TODAY
Dễ : So sánh các số hữu tỉ
Khó : Giả sử
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
thì ta có x < z < y
Giả sử x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\)(a, b, m \(\in\) Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì ta có x < z < y
Hướng dẫn: Sử dụng tính chất: Nếu a, b, c \(\in\) Z và a < b thì a + c < b + c
Giúp mk nốt câu này nhé
Giả sử \(x=\dfrac{a}{m};y=\dfrac{b}{m}\left(a,b,m\in Z,m>0\right)\) và \(x< y\).
Hãy chứng tỏ rằng nếu chọn \(z=\dfrac{a+b}{2m}\) thì ta có \(x< z< y\).
Giả sử\(x=\dfrac{a}{m},y=\dfrac{b}{m}\left(a;b;m\in Z,m>0\right)\) và x < y. Hãy chứng tỏ rằng nếu chọn z=\(\dfrac{a+b}{2m}\) thì ta có x < z <y
Giả sử x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\) (a, b, m ∈ Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì ta có x < z < y.
Hướng dẫn. Sử dụng tính chất: Nếu a, b, c ∈ Z và a < b thì a + c < b + c.
Giả sử \(x=\dfrac{a}{m},y=\dfrac{b}{m}\left(a,b,m\in Z,m\ne0\right)\) và x < y . Hãy chứng tỏ rằng nếu chọn \(z=\dfrac{a+b}{2m}\) thì ta có x < z < y.
Hướng dẫn : Sử dụng tính chất : Nếu \(a,b,c\in Z\) và a < b thì a + c < b + c .
cho các số hữu tỉ x=a/b; y= c/d ; b > 0 ; d< 0 và các số tự nhiên m,n với m # 0 . chứng minh rằng:
nếu a/b < c/d thì a/b < ma + nc / mb + nd < c/d
help me
Bài 1
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ frac{3}{-4} :
frac{-12}{15}, frac{-15}{20}, frac{24}{-32}, frac{-20}{28}, frac{-27}{36} ?
b) Biểu diễn số hữu tỉ frac{3}{-4} trên trục số.
Bài 2
So sánh các số hữu tỉ :
a) x frac{2}{-7} và y frac{-3}{11}
b) x frac{-213}{300} và y frac{18}{-25}
c) x -0,75 và y frac{-3}{4}
Bài 3
So sánh số hữu tỉ frac{a}{b} (a, b, ∈ Z, b ≠ 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu.
Bài 4
Giả sử x , y (a, b, m ∈ Z, m...
Đọc tiếp
Bài 1
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ \(\frac{3}{-4}\) :
\(\frac{-12}{15}\), \(\frac{-15}{20}\), \(\frac{24}{-32}\), \(\frac{-20}{28}\), \(\frac{-27}{36}\) ?
b) Biểu diễn số hữu tỉ \(\frac{3}{-4}\) trên trục số.
Bài 2
So sánh các số hữu tỉ :
a) x = \(\frac{2}{-7}\) và y = \(\frac{-3}{11}\)
b) x = \(\frac{-213}{300}\) và y = \(\frac{18}{-25}\)
c) x = \(-0,75\) và y = \(\frac{-3}{4}\)
Bài 3
So sánh số hữu tỉ \(\frac{a}{b}\) (a, b, ∈ Z, b ≠ 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu.
Bài 4
Giả sử x = , y = (a, b, m ∈ Z, m > 0) và x < y). Hãy chứng tỏ rằng nếu chọn z = \(\frac{a+b}{2m}\) thì ta có x < z < y.
Hướng dẫn: Sử dụng tính chất : Nếu a, b, c ∈ Z và a < b thì a + c < b + c.
Bài 5 ( SGK toán 7 tập 1 / trang 8)
Giả sử xdfrac{a}{m} , ydfrac{b}{m}left(a,b,min Z,m0right) và x y. Hãy chứng tỏ rằng nếu chọn zdfrac{a+b}{2m} thì ta có x z y.
Hướng dẫn: Sử dụng tính chất: Nếu a,b,cin Z và a b thì a+c b+c.
Đọc tiếp
Bài 5 ( SGK toán 7 tập 1 / trang 8)
Giả sử \(x=\dfrac{a}{m}\) , \(y=\dfrac{b}{m}\left(a,b,m\in Z,m>0\right)\) và \(x< y\). Hãy chứng tỏ rằng nếu chọn \(z=\dfrac{a+b}{2m}\) thì ta có \(x< z< y\).
Hướng dẫn: Sử dụng tính chất: Nếu \(a,b,c\in Z\) và \(a< b\) thì \(a+c< b+c\).

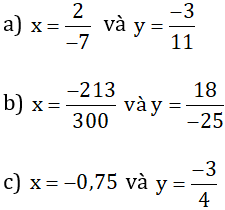
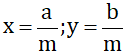 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 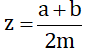 thì ta có x < z < y.
thì ta có x < z < y.










