Vì x < y nên ta có:
\(\dfrac{a}{m}< \dfrac{b}{m}\)
\(\Rightarrow\dfrac{a}{m}< \dfrac{a+b}{m+m}< \dfrac{b}{m}\)
\(\Rightarrow\dfrac{a}{m}< \dfrac{a+b}{2m}< \dfrac{b}{m}\)
\(\Rightarrow x< z< y\left(đpcm\right)\)
Vậy \(x< z< y\)
Vì x < y nên ta có:
\(\dfrac{a}{m}< \dfrac{b}{m}\)
\(\Rightarrow\dfrac{a}{m}< \dfrac{a+b}{m+m}< \dfrac{b}{m}\)
\(\Rightarrow\dfrac{a}{m}< \dfrac{a+b}{2m}< \dfrac{b}{m}\)
\(\Rightarrow x< z< y\left(đpcm\right)\)
Vậy \(x< z< y\)
Giả sử x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\)(a, b, m \(\in\) Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì ta có x < z < y
Hướng dẫn: Sử dụng tính chất: Nếu a, b, c \(\in\) Z và a < b thì a + c < b + c
Giúp mk nốt câu này nhé
Giả sử \(x=\dfrac{a}{m},y=\dfrac{b}{m}\left(a,b,m\in Z,m\ne0\right)\) và x < y . Hãy chứng tỏ rằng nếu chọn \(z=\dfrac{a+b}{2m}\) thì ta có x < z < y.
Hướng dẫn : Sử dụng tính chất : Nếu \(a,b,c\in Z\) và a < b thì a + c < b + c .
Giả sử\(x=\dfrac{a}{m},y=\dfrac{b}{m}\left(a;b;m\in Z,m>0\right)\) và x < y. Hãy chứng tỏ rằng nếu chọn z=\(\dfrac{a+b}{2m}\) thì ta có x < z <y
Giả sử \(x=\dfrac{a}{m};y=\dfrac{b}{m}\left(a,b,m\in Z,m>0\right)\) và \(x< y\).
Hãy chứng tỏ rằng nếu chọn \(z=\dfrac{a+b}{2m}\) thì ta có \(x< z< y\).
Giả sử x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\) (a, b, m ∈ Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì ta có x < z < y.
Hướng dẫn. Sử dụng tính chất: Nếu a, b, c ∈ Z và a < b thì a + c < b + c.
Câu Hỏi Today
Dễ : So sánh các số hữu tỉ
Khó : Giả sử 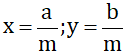
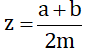
Câu Hỏi YESTERDAY AND TODAY
Dễ : So sánh các số hữu tỉ
Khó : Giả sử
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
thì ta có x < z < y
Bài 1
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ \(\frac{3}{-4}\) :
\(\frac{-12}{15}\), \(\frac{-15}{20}\), \(\frac{24}{-32}\), \(\frac{-20}{28}\), \(\frac{-27}{36}\) ?
b) Biểu diễn số hữu tỉ \(\frac{3}{-4}\) trên trục số.
Bài 2
So sánh các số hữu tỉ :
a) x = \(\frac{2}{-7}\) và y = \(\frac{-3}{11}\)
b) x = \(\frac{-213}{300}\) và y = \(\frac{18}{-25}\)
c) x = \(-0,75\) và y = \(\frac{-3}{4}\)
Bài 3
So sánh số hữu tỉ \(\frac{a}{b}\) (a, b, ∈ Z, b ≠ 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu.
Bài 4
Giả sử x = , y = (a, b, m ∈ Z, m > 0) và x < y). Hãy chứng tỏ rằng nếu chọn z = \(\frac{a+b}{2m}\) thì ta có x < z < y.
Hướng dẫn: Sử dụng tính chất : Nếu a, b, c ∈ Z và a < b thì a + c < b + c.
CÂU LẠC BỘ TOÁN HỌC
CHỦ NHIỆM: PHAN NGỌC THANH TRÂM
ĐỀ BÀI:
I. PHẦN LÝ THUYẾT:
1. Số hữu tỉ
Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b \in \mathbb Z, b \ne 0\) và được kí hiệu là \(\mathbb Q\)
2. Biểu diễn số hữu tỉ trên trục số
Mỗi số hữu tỉ được biểu diễn bởi một điểm trên trục số và không phụ thuộc vào cách chọn phân số xác định nó.
3. So sánh số hữu tỉ
Để so sánh hai số hữu tỉ \(x,y\) ta làm như sau:
- Viết \(x,y\) dưới dạng phân số cùng mẫu dương.
\(x = \dfrac{a}{m} ; y = \dfrac{b}{m} ( m>0)\)
- So sánh các tử là số nguyên \(a\) và \(b\)
Nếu \(a> b\) thì \(x > y\)
Nếu \(a = b\) thì \(x=y\)
Nếu \(a < b\) thì \(x < y\).
4. Chú ý
- Số hữu tỉ lớn hơn \(0\) gọi là số hữu tỉ dương
- Số hữu tỉ nhỏ hơn \(0\) gọi là số hữu tỉ âm
- Số \(0\) không là số hữu tỉ dương, cũng không là số hữu tỉ âm
II. PHẦN BÀI TẬP:
A. Trắc nghiệm:
Câu 1: Định nghĩa số hữu tỉ?
A. Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b \in \mathbb Z, b \ne 0\) và được kí hiệu là \(\mathbb Q\)
B. Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b \in \mathbb Z, b = 0\) và được kí hiệu là \(\mathbb Q\)
C. Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b \in \mathbb N, b \ne 0\) và được kí hiệu là \(\mathbb Q\)
D. Số hữu tỉ là số có thể viết dưới dạng \(\dfrac{a}{b}\) với \(a, b \in \mathbb R, b \ne 0\) và được kí hiệu là \(\mathbb Q\)
Câu 2: Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ \(\dfrac{3}{-4}\)
A.\(- \dfrac{12}{15}\)
B. \(- \dfrac{20}{8}\)
C. \(-\dfrac{18}{12}\)
D. \(-\dfrac{15}{20}\)
Câu 3: Tập hợp số hữu tỉ được kí hiệu là:
A. \(\mathbb Q\)
B. \(\mathbb N\)
C. \(\mathbb R\)
D. \(\mathbb Z\)
Câu 4: Khẳng định nào sau đây là đúng:
A. Số \(0\) không là số hữu tỉ dương
B Số \(0\) không là số hữu tỉ âm
C. Số \(0\) không là số hữu tỉ dương, cũng không là số hữu tỉ âm
D. Số \(0\) là số hữu tỉ
Câu 5: Cách viết nào sau đây là đúng:
A. \(\dfrac{3}{2} \in \mathbb Q\)
B. \(\dfrac{2}{3} \in \mathbb Z\)
C. \(-\dfrac{9}{2} \notin \mathbb Q\)
D. \(-6 \in \mathbb N\)
Câu 6: Số nào sau đây là số hữu tỉ dương:
A.\(\dfrac{-2}{-3}\)
B. \(\dfrac{-2}{5}\)
C. \(\dfrac{-5}{15}\)
D. \(\dfrac{-2}{15}\)
II.TỰ LUẬN:
Câu 1: So sánh các số hữu tỉ:
a) \(x = \dfrac{2}{-7}\) và \(y = \dfrac{-3}{11}.\)
b) \(x = \dfrac{-213}{300}\) và \(y = \dfrac{18}{-25}.\)
c) \(x = -0,75\) và \(y = \dfrac{-3}{4}.\)
Câu 2:
a) Biểu diễn các số hữu tỉ sau trên trục số: \(\dfrac{2}{5};\dfrac{{- 4}}{5};\dfrac{7}{5}\)
b) Hãy sắp xếp các số hữu tỉ sau theo thứ tự tăng dần: \(\dfrac{9}{{11}};\dfrac{{ - 30}}{{ - 40}};0;\dfrac{{ - 14}}{{18}};\dfrac{{ - 12}}{{ - 8}}\)
Câu 3: Cho số hữu tỉ \(x=\dfrac{a - 4}{5}\), với giá trị nào của a thì:
a) x là số dương?
b) x là số âm?
c) x không là số dương cũng không là số âm?
Câu 4: Cho số hữu tỉ \(x=\dfrac{a + 17}{a}\) ( \(a ≠ 0\) ). Với giá trị nguyên nào của a thì x là số nguyên?
Sưu tầm và biên soạn: PCN: Nguyễn Thành Trương