Giải 1+2cos2x=sin2x

Những câu hỏi liên quan
Giải phương trình :
sin2x -\(\dfrac{\sqrt{3}}{2}\)sin2x+ 2cos2x =1
Thấy cosx= 0 là nghiệm của phương trình => \(x=\dfrac{\pi}{2}+k\pi\)
Xét cosx khác 0, chia cả 2 vế cho cos^2 x
\(\Leftrightarrow\tan^2x-\sqrt{3}\tan x+2=1+\tan^2x\)
\(\Leftrightarrow\tan x=\dfrac{\sqrt{3}}{3}\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đúng 0
Bình luận (0)
Giải: (2cos2x-1).(sin2x+cos2x)=1
Giải pt (2cos2x-1)(sin2x+cos2x)=1
P/t \(\Leftrightarrow2cos2x.sin2x-sin2x+2cos^22x-cos2x-1=0\)
\(\Leftrightarrow sin4x-sin2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sinx.cos3x-2sin3x.sinx=0\)
\(\Leftrightarrow sinx\left(cos3x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\left(1\right)\\cos3x=sin3x\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow x=k\pi\left(k\in Z\right)\)
(2) \(\Leftrightarrow sin3x-cos3x=0\) \(\Leftrightarrow\sqrt{2}sin\left(3x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow3x-\dfrac{\pi}{4}=k\pi\Leftrightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\left(k\in Z\right)\)
Vậy ...
Đúng 0
Bình luận (0)
Giải phương trình sau: 2 cos 2 x - 3 sin 2 x + sin 2 x = 1
2 cos 2 x - 3 sin 2 x + sin 2 x = 1
- cosx = 0 thỏa mãn phương trình ⇒ phương trình có nghiệm x = π/2+kπ,k ∈ Z.
- Với cosx ≠ 0, chia hai vế cho cos 2 x , tìm được tanx = 1/6.
Vậy phương trình có các nghiệm x = π/2+kπ,k ∈ Z và x = arctan1/6 + kπ,k ∈ Z.
Đúng 0
Bình luận (0)
Giải: \(\left(2cos2x-1\right).\left(sin2x+cos2x\right)=1\)
=>\(2\cdot cos2x\cdot sin2x+2cos^22x-sin2x-cos2x-1=0\)
=>\(2cos2x\cdot sin2x+2\cdot cos^22x-1=sin2x+cos2x\)
=>\(sin4x+cos4x=sin2x+cos2x\)
=>\(sin\left(4x+\dfrac{pi}{4}\right)=sin\left(2x+\dfrac{pi}{4}\right)\)
=>4x+pi/4=2x+pi/4+k2pi hoặc 4x+pi/4=pi-2x-pi/4+k2pi
=>2x=k2pi hoặc 6x=1/2pi+k2pi
=>x=kpi hoặc x=1/12pi+kpi/3
Đúng 1
Bình luận (0)
Giải phương trình:
\(\left(2Cos2x-1\right)\left(Sin2x+Cos2x\right)=1\)
\(\left(2cos2x-1\right)\left(sin2x+cos2x\right)=1\)
\(\Leftrightarrow2sin2x.cos2x+2cos^22x-sin2x-cos2x-1=0\)
\(\Leftrightarrow sin4x+cos4x-sin2x-cos2x=0\)
\(\Leftrightarrow2cos3x.sinx-2sin3x.sinx=0\)
\(\Leftrightarrow2sinx\left(cos3x-sin3x\right)=0\)
\(\Leftrightarrow2\sqrt{2}sinx.cos\left(3x+\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos\left(3x+\dfrac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\3x+\dfrac{\pi}{4}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải các phương trình sau: 1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0
1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0 ( 1 ) T a c ó : 1 - sin 2 x = sin x - cos x 2 ⇔ 2 cos 2 x = 2 ( cos 2 x - sin 2 x ) = - 2 ( sin x - cos x ) ( sin x + cos x ) V ậ y ( 1 ) ⇔ ( sin x - cos x ) ( 1 + sin x - cos x - 2 sin x - 2 cos x ) = 0 ⇔ ( sin x - cos x ) ( 1 - sin x - 3 cos x ) = 0
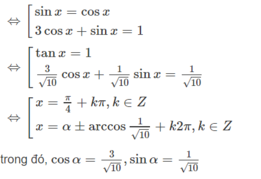
Đúng 0
Bình luận (0)
Giải phương trình:
sin4x + sin2x + 2cos2x = -1
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
















