Cho \(x\ne0;y\ne0\) thỏa mãn:\(x+y=4,x.y=2\)
Giá trị của biểu thức \(A=\frac{1}{x^3}+\frac{1}{y^3}\) là A=...?
Chọn chữ cái đứng trước câu trả lời đúng cho mỗi câu hỏi dưới đây
Câu 1: Điều kiện xác định của phương trình \(\dfrac{x-2}{x\left(x-2\right)}=0\) là:
A. \(x\ne0\) B. \(x\ne2\) C. \(x\ne0;x\ne-2\) D. \(x\ne0;x\ne2\)
Câu 2: Trong các phương trình sau phương trình nào là phương trình bậc nhất 1 ẩn?
A. x + \(x^2\)= 0
B. 1 -2x = 0
C. 0x + 4 = 0
D. \(\dfrac{1}{x-2}=0\)
Câu 3: Trong các cặp phương trình sau, cặp nào là 2 phương trình tương đương?
A. 3x-3 và x-1=0
B. x-3=0 và 3x+9=0
C. x-2=0 và (x-2)(x+3)=0
D. \(x^2+2=0vàx\left(x^2+2\right)=0\)
Câu 4: Trong các khẳng định sau, khẳng định nào đúng?
A) A(x) + B(x) = 0 \(\Leftrightarrow\)A(x) = 0 và B(x) = 0
B) A(x) . B(x) = 0 \(\Leftrightarrow\)A(x) = 0 và B(x) = 0
C) A(x) . B(x) = 0 \(\Leftrightarrow\)A(x) = 0 hoặc B(x) = 0
D) A(x) : B(x) = 0 \(\Leftrightarrow\)A(x) = 0 và B(x) = 0
Câu 5: Cho AB = 1,5 dm; CD = 30 cm. Tỉ số của hai đoạn thẳng AB và CD là:
A. \(\dfrac{1,5}{30}\) B. \(\dfrac{30}{1,5}\) C. 2 D. \(\dfrac{1}{2}\)
Câu 7: Cho \(\Delta\)ABC có AB =6cm ; AC = 8 cm; AD là phân giác trong \(\left(D\in BC\right)\). Hãy chọn đáp án đúng
A. \(\dfrac{BD}{DC}=\dfrac{4}{5}\) B. \(\dfrac{DB}{DC}=\dfrac{5}{3}\) C. \(\dfrac{DB}{DC}=\dfrac{3}{4}\) D. \(\dfrac{DB}{DC}=\dfrac{4}{3}\)
Câu 8: Cho hình vẽ sau, biết MN // QR. Độ dài x của đoạn thẳng QR có giá trị là:
A. x = 3 B. x = 4 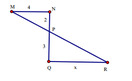
C. x = 5 D. x = 6
Câu 1: D
Câu 2: B
Câu 3: D
Câu 4: C
Câu 5: A
Cho x,y,z là 3 số thỏa mãn \(x+y\ne0;y+z\ne0;z+x\ne0\) . Tính giá tri biểu thức\(A=\frac{y+z}{x}+\frac{z+x}{y}+\frac{x+y}{z}\)
Cho \(a+b+c=a^2+b^2+c^2=1\) và \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) \(\left(a\ne0,b\ne0,c\ne0\right)\)
Chứng minh rằng: \(\left(x+y+z\right)^2=x^2+y^2+z^2\)
Lời giải:
Đặt $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=t$
$\Rightarrow x=at; y=bt; z=ct$. Ta có:
$(x+y+z)^2=(at+bt+ct)^2=t^2(a+b+c)^2=t^2(*)$
Mặt khác:
$x^2+y^2+z^2=(at)^2+(bt)^2+(ct)^2=t^2(a^2+b^2+c^2)=t^2(**)$
Từ $(*); (**)\Rightarrow (x+y+z)^2=x^2+y^2+z^2$ (đpcm)
Cho x,y,z là 3 số thỏa mãn \(x+y\ne0;y+z\ne0;x+z\ne0\) . Tính giá tri biểu thức \(A=\frac{y+z}{x}+\frac{x+z}{y}+\frac{x+y}{z}\)
link nè:
Câu hỏi của Cao Thành Lộc - Toán lớp 7 - Học toán với OnlineMath
Giúp mk nhanh nha![]() , mai mk phải kiểm tra rùi
, mai mk phải kiểm tra rùi![]()
Cho 3x-y=3z và 2x+y=7z. Tính giá trị của biểu thức: \(M=\dfrac{x^2-2xy}{x^2+y^2}\left(x\ne0,y\ne0\right)\)
Ta có: \(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Leftrightarrow3x-y+2x+y=10z\)
\(\Leftrightarrow5x=10z\)
hay x=2z
Thay x=2z vào biểu thức 3x-y=3z, ta được:
\(3\cdot2z-y=3z\)
\(\Leftrightarrow6z-y=3z\)
hay y=3z
Thay x=2z và y=3z vào biểu thức \(M=\dfrac{x^2-2xy}{x^2+y^2}\), ta được:
\(M=\dfrac{\left(2z\right)^2-2\cdot2z\cdot3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{13z^2}=\dfrac{-8z^2}{13z^2}=\dfrac{-8}{13}\)
Vậy: \(M=\dfrac{-8}{13}\)
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)
Cho \(abc\ne0\) và \(a+b+c\ne0\). Tìm \(x\), biết: \(\dfrac{a+b-x}{c}+\dfrac{a+c-x}{b}+\dfrac{b+c-x}{a}+\dfrac{4x}{a+b+c}=1\)
Lời giải:
PT $\Leftrightarrow \frac{a+b-x}{c}+1+\frac{a+c-x}{b}+1+\frac{b+c-x}{a}+1+\frac{4x}{a+b+c}-4=0$
$\Leftrightarrow \frac{a+b+c-x}{c}+\frac{a+b+c-x}{b}+\frac{a+b+c-x}{a}-\frac{4(a+b+c-x)}{a+b+c}=0$
$\Leftrightarrow (a+b+c-x)(\frac{1}{c}+\frac{1}{b}+\frac{1}{a}-\frac{4}{a+b+c})=0$
$\Rightarrow a+b+c-x=0$ hoặc $\frac{1}{c}+\frac{1}{b}+\frac{1}{a}-\frac{4}{a+b+c}=0$
Nếu $\frac{1}{c}+\frac{1}{b}+\frac{1}{a}-\frac{4}{a+b+c}=0$, khi đó $x$ nhận mọi giá trị thực.
Nếu $\frac{1}{c}+\frac{1}{b}+\frac{1}{a}-\frac{4}{a+b+c}\neq 0$
$\Rightarrow a+b+c-x=0$
$\Rightarrow x=a+b+c$
Cho số thực x và y thỏa mãn \(x\ne y;x\ne0;y\ne0\)
CMR: \(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)
\(VT=\dfrac{1}{\left(x-y\right)^2}+\dfrac{x^2+y^2}{x^2y^2}=\dfrac{1}{\left(x-y\right)^2}+\dfrac{\left(x-y\right)^2+2xy}{x^2y^2}\)
\(VT=\dfrac{1}{\left(x-y\right)^2}+\dfrac{\left(x-y\right)^2}{x^2y^2}+\dfrac{2}{xy}\ge2\sqrt{\dfrac{\left(x-y\right)^2}{\left(x-y\right)^2x^2y^2}}+\dfrac{2}{xy}=\dfrac{2}{\left|xy\right|}+\dfrac{2}{xy}\ge\dfrac{2}{xy}+\dfrac{2}{xy}=\dfrac{4}{xy}\)
Vận dụng tính chất dãy tỉ số bằng nhau:
a)Cho \(ac=b^2;ab=c^2;a+b+c\ne0;a,b,c\ne0\)
Tính:\(P=\frac{b^{333}}{a^{111}\cdot c^{222}}\)
b)Cho \(x^2=yz;y^2=xz;x+y+z\ne0;xyz\ne0\)
a) \(ac=b^2\Rightarrow\frac{a}{b}=\frac{b}{c}\)
\(ab=c^2\Rightarrow\frac{a}{c}=\frac{c}{b}\)
Suy ra: \(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{a+b+c}=1\)
\(P=\frac{b^{333}}{a^{111}.c^{222}}=\frac{b^{333}}{a^{111}.c^{111}.c^{111}}=\frac{b^{333}}{\left(ac\right)^{111}.c^{111}}=\frac{b^{333}}{\left(b^2\right)^{111}.c^{111}}=\frac{b^{333}}{b^{222}.c^{111}}=\frac{b^{111}}{c^{111}}=\left(\frac{b}{c}\right)^{111}\)
\(=1^{111}=1\)
Cho \(x\ne0\), \(y\ne0\), \(z\ne0\), \(\frac{1}{x}-\frac{1}{y}-\frac{1}{z}\) = 1 và x = y + z
Chứng minh rằng : \(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\) = 1
Giúp mình vớiiiiiiiiiiiiii
Điều kiện xác định của phương trình\(\dfrac{x+2}{x-3}=\dfrac{3x-1}{x\left(x-3\right)}+1\)
A.\(x\ne0;x\ne3\)
B.\(x\ne0;x\ne-3\)
C.\(x\ne0\)
D.\(x\ne\pm3\)
Điều kiện xác định là `{(x-3 ne 0),(x(x-3) ne 0):}`
`<=>{(x ne 3),(x ne 0):}`
`=>bb A`
ĐCXĐ: \(\left\{{}\begin{matrix}x\ne0\\x-3\ne0\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x\ne0\\x\ne3\end{matrix}\right.\)