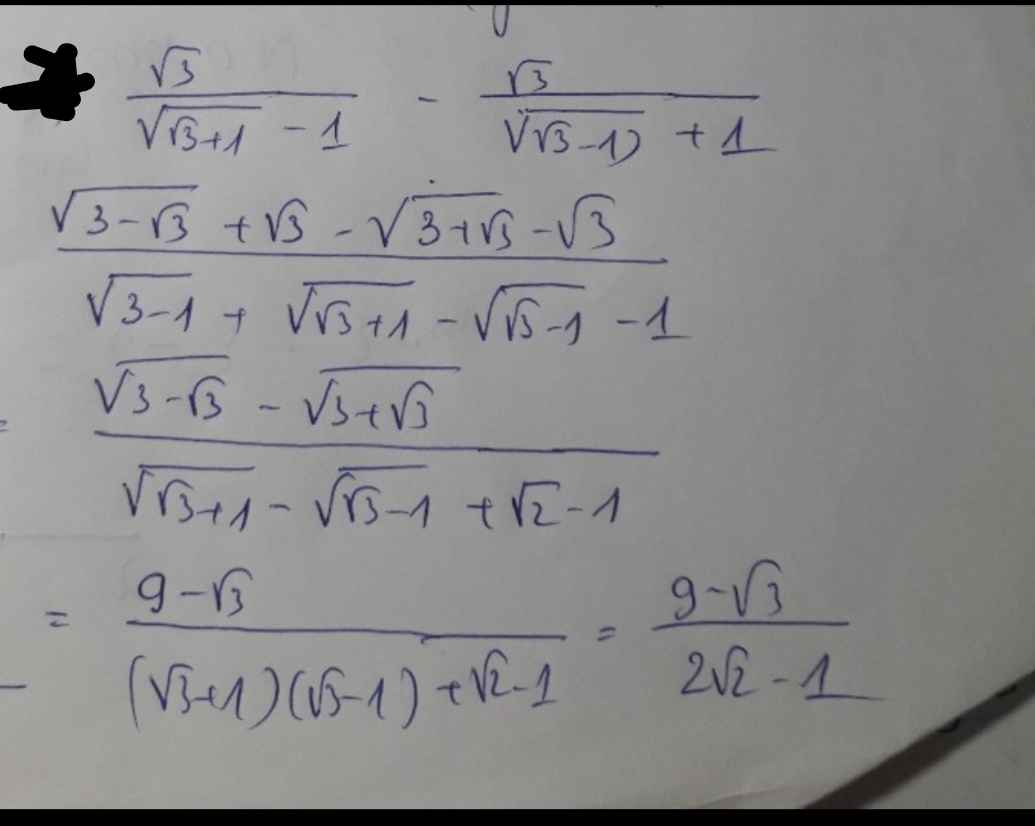Ta có: \(\dfrac{3\sqrt{\sqrt{3}-1}}{\sqrt{\sqrt{3}-1}-3}\)

\(=\dfrac{3\sqrt{\sqrt{3}-1}\left(\sqrt{\sqrt{3}-1}+3\right)}{\sqrt{3}-4}\)

\(=3\cdot\dfrac{\left(\sqrt{3}-1+3\sqrt{\sqrt{3}-1}\right)}{\sqrt{3}-4}\)

\(=\dfrac{-3\left(\sqrt{3}+4\right)\left(\sqrt{3}-1+3\sqrt{\sqrt{3}-1}\right)}{13}\)

Lời giải:

a) ĐK: $x\geq 0; y\geq 0; x\neq y$

\(A=\left[\frac{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}{\sqrt{x}-\sqrt{y}}-\frac{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}\right]:\frac{x-\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)

\(=\left(\sqrt{x}+\sqrt{y}-\frac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\right).\frac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}\)

\(=\frac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}.\frac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}=\frac{\sqrt{xy}}{x-\sqrt{xy}+y}\)

b) \(1-A=\frac{(\sqrt{x}-\sqrt{y})^2}{x-\sqrt{xy}+y}>0\) với mọi $x\neq y; x,y\geq 0$

$\Rightarrow A< 1$

đừng để ý cái đen đen🥲

Ta có: \(\sqrt{12}-\dfrac{3+\sqrt{3}}{\sqrt{3}+1}+\dfrac{11}{2\sqrt{3}+1}\)

\(=2\sqrt{3}-\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}+\dfrac{11\left(2\sqrt{3}-1\right)}{\left(2\sqrt{3}+1\right)\left(2\sqrt{3}-1\right)}\)

\(=2\sqrt{3}-\sqrt{3}+\left(2\sqrt{3}-1\right)\)

\(=\sqrt{3}+2\sqrt{3}-1\)

\(=3\sqrt{3}-1\)

Ta có : \(\sqrt{12}-\dfrac{3+\sqrt{3}}{\sqrt{3}+1}+\dfrac{11}{2\sqrt{3}+1}\)

\(=\sqrt{12}-\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}+\dfrac{\left(2\sqrt{3}+1\right)\left(2\sqrt{3}-1\right)}{2\sqrt{3}+1}\)

\(=\sqrt{12}-\sqrt{3}+2\sqrt{3}-1=2\sqrt{3}-\sqrt{3}+2\sqrt{3}-1\)

\(=3\sqrt{3}-1\)

\(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}-1}+1}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}+1\right)}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}-1}-1\right)}{\sqrt{3}}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}-\sqrt{\sqrt{3}-1}+2\right)}{\sqrt{3}}=\sqrt{\sqrt{3}+1}-\sqrt{\sqrt{3}-1}+2\)

\(\frac{1}{\sqrt{2}-\sqrt{3}}-\frac{1}{\sqrt{3}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{7}}\)

= \(-\sqrt{3}-\sqrt{2}+\frac{\sqrt{5}+\sqrt{3}}{2}-\frac{\sqrt{7}+\sqrt{5}}{2}\)

= \(-\sqrt{3}-\sqrt{2}+\frac{\sqrt{3}-\sqrt{7}}{2}\)

= \(\frac{-2\sqrt{3}-2\sqrt{2}+\sqrt{3}-\sqrt{7}}{2}=\frac{-\sqrt{3}-2\sqrt{2}-\sqrt{7}}{2}\)

Chúc bạn học tốt !!!

Lời giải:
\(\frac{1}{1-\sqrt{2}}-\frac{1}{\sqrt{2}-\sqrt{3}}+\frac{1}{\sqrt{3}-\sqrt{4}}=\frac{1+\sqrt{2}}{(1-\sqrt{2})(1+\sqrt{2})}-\frac{\sqrt{2}+\sqrt{3}}{(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})}+\frac{\sqrt{3}+\sqrt{4}}{(\sqrt{3}-\sqrt{4})(\sqrt{3}+\sqrt{4})}\)

\(=\frac{1+\sqrt{2}}{1-2}-\frac{\sqrt{2}+\sqrt{3}}{2-3}+\frac{\sqrt{3}+\sqrt{4}}{3-4}=-(1+\sqrt{2})+(\sqrt{2}+\sqrt{3})-(\sqrt{3}+\sqrt{4})\)

\(=-1-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}=-1-\sqrt{4}=-1-2=-3\)

\(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}\)

\(=\dfrac{\sqrt{2}+1}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}-\dfrac{\sqrt{2}+\sqrt{3}}{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{3}\right)}+\dfrac{\sqrt{4}+\sqrt{3}}{\left(\sqrt{3}-\sqrt{4}\right)\left(\sqrt{3}+\sqrt{4}\right)}\)

\(=\dfrac{\sqrt{2}+1}{-1}-\dfrac{\sqrt{2}+\sqrt{3}}{-1}+\dfrac{\sqrt{4}+\sqrt{3}}{-1}=-1-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{4}-\sqrt{3}\)

\(=-1-\sqrt{4}=-1-2=-3\)

\(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}\)

\(=-\sqrt{2}-1+\sqrt{3}+\sqrt{2}-2-\sqrt{3}\)

=-3