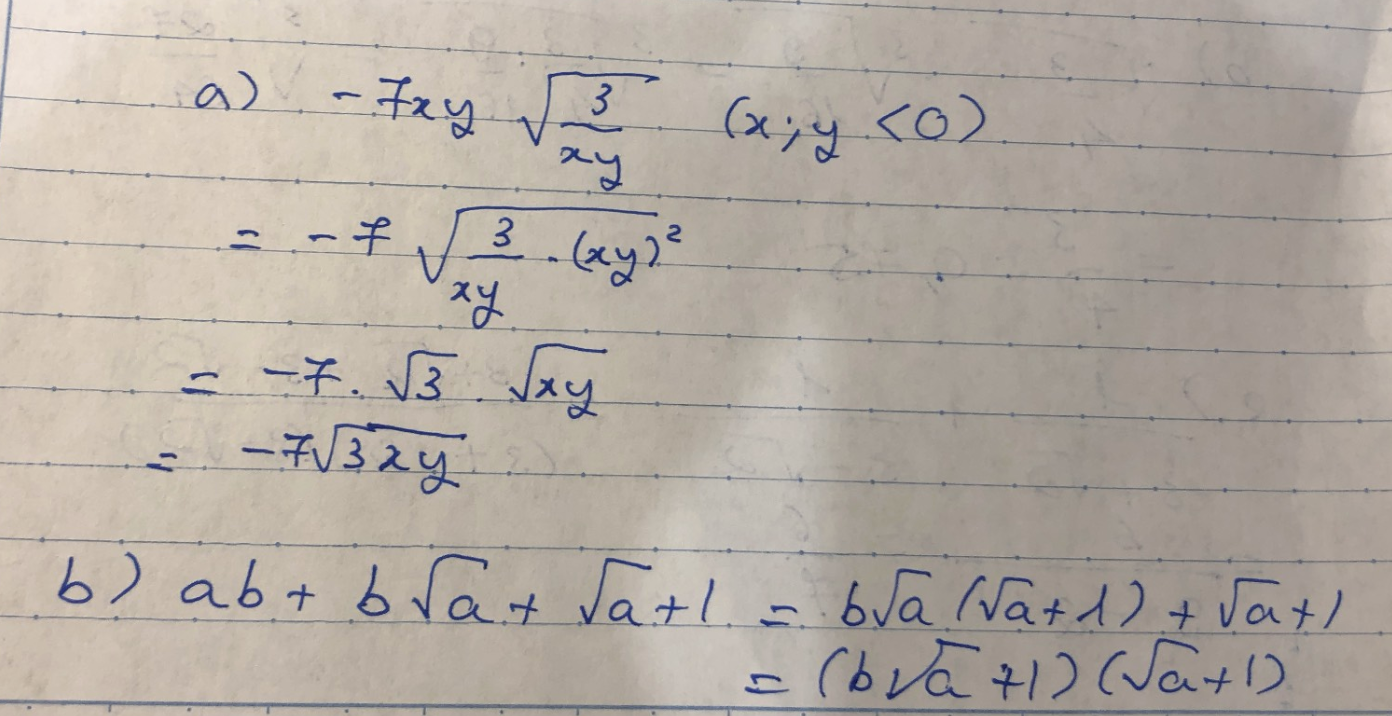Rút gọn biểu thức \(A=\dfrac{\sqrt{x^6y^2}}{xy}\) với x<0, y>0

Những câu hỏi liên quan
\(P=\left(\sqrt{x}+\dfrac{y-\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\right)\):\(\left(\dfrac{x}{\sqrt{xy}+y}+\dfrac{y}{\sqrt{xy}-x}-\dfrac{x+y}{\sqrt{xy}}\right)\)
a) Với giá trị nào cùa x thì biểu thức có nghĩa
b) Rút gọn P
c) Tím P với x=3 và y=\(\dfrac{2}{2-\sqrt{3}}\)
Giúp với ạ
Cho biểu thức:
A = (\(\sqrt{x}\) + \(\dfrac{y-\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)) : (\(\dfrac{x}{\sqrt{xy}+y}\) + \(\dfrac{y}{\sqrt{xy}-x}\) - \(\dfrac{x+y}{\sqrt{xy}}\))
a) Rút gọn A
b) Tính giá trị của biểu thức A biết x = 3; y = 4 + 2\(\sqrt{3}\)
1.Thực hiện phép tính: 2.Tìm x biết: 2sqrt{36x-36}-dfrac{1}{3}sqrt{9x-9}-4sqrt{4x-4}+sqrt{x-1}163. Cho biểu thức: ( với x0; x1)a) Rút gọn biểu thức Pb) Xác định x để 4.Cho tam giác ABC vuông tại A, đường cao AH6cm, HC 8cm.a)Tính độ dài HB,BC, AB, ACb)Kẻ . Tính độ dài HD và diện tích tam giác AHD5. Giải tam giác vuông ABC vuông tại A, biết AC 8cm, và
Đọc tiếp
1.Thực hiện phép tính:
2.Tìm x biết:
\(2\sqrt{36x-36}-\dfrac{1}{3}\sqrt{9x-9}-4\sqrt{4x-4}+\sqrt{x-1}=16\)
3. Cho biểu thức: ( với x
![]() 0; x
0; x![]() 1)
1)
a) Rút gọn biểu thức P
b) Xác định x để
4.
Cho tam giác ABC vuông tại A, đường cao AH=6cm, HC= 8cm.
a)Tính độ dài HB,BC, AB, AC
b)Kẻ . Tính độ dài HD và diện tích tam giác AHD
5. Giải tam giác vuông ABC vuông tại A, biết AC = 8cm, và
\(=2\sqrt{3}-4\sqrt{3}+5\sqrt{3}=3\sqrt{3}\)
Đúng 2
Bình luận (0)
Bài 5:
\(\widehat{B}=60^0\)
\(AB=8\sqrt{3}\left(cm\right)\)
\(BC=16\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho biểu thức B = \(\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
a) Rút gọn biểu thức B
b) Chứng minh \(B\ge0\)
a) \(B=\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\left(x,y\ge0;x\ne y\right)\)
\(B=\left[\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}-\dfrac{\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3}{x-y}\right]:\dfrac{x-2\sqrt{xy}+y+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
\(B=\left[\left(\sqrt{x}+\sqrt{y}\right)-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\right]:\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)
\(B=\left[\left(\sqrt{x}+\sqrt{y}\right)-\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\right]:\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)
\(B=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)
\(B=\dfrac{x+2\sqrt{xy}+y-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)
\(B=\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)
\(B=\dfrac{\sqrt{xy}}{x+\sqrt{xy}+y}\)
b) Xét tử:
\(\sqrt{xy}\ge0\forall x,y\) (xác định) (1)
Xét mẫu:
\(x+\sqrt{xy}+y\)
\(=\left(\sqrt{x}\right)^2+2\cdot\dfrac{1}{2}\sqrt{y}\cdot\sqrt{x}+\left(\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y\)
Mà: \(\left(\sqrt{x}+\dfrac{1}{2}\sqrt{y}\right)^2\ge0\forall x,y\) (xác định), còn: \(\dfrac{3}{4}y\ge0\) vì theo đkxđ thì \(y\ge0\) (2)
Từ (1) và (2) ⇒ B luôn không âm với mọi x,y (\(B\ge0\)) (đpcm)
Đúng 4
Bình luận (0)
rút gọn biểu thức A=\(\dfrac{x+\sqrt{y}+\sqrt{xy}-1}{\sqrt{x}+1}:(\sqrt{x}-\sqrt{y})\)
Lời giải:
\(A=\frac{(x-1)+(\sqrt{y}+\sqrt{xy})}{\sqrt{x}+1}.\frac{1}{\sqrt{x}-\sqrt{y}}\\ =\frac{(\sqrt{x}-1)(\sqrt{x}+1)+\sqrt{y}(\sqrt{x}+1)}{\sqrt{x}+1}.\frac{1}{\sqrt{x}-\sqrt{y}}\\ =\frac{(\sqrt{x}+1)(\sqrt{x}-1+\sqrt{y})}{\sqrt{x}+1}.\frac{1}{\sqrt{x}-\sqrt{y}}\\ =\frac{\sqrt{x}+\sqrt{y}-1}{\sqrt{x}-\sqrt{y}}\)
Đúng 1
Bình luận (0)
\(A=\dfrac{x+\sqrt{y}+\sqrt{xy}-1}{\sqrt{x}+1}:\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\dfrac{\left(x-1\right)+\sqrt{y}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}:\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)+\sqrt{y}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}:\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\dfrac{\left(\sqrt{x}-1+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}\)
Đúng 0
Bình luận (0)
a. Khử mẫu của biểu thức sau rồi rút gọn:-7xy.\(\sqrt{\dfrac{3}{xy}}\)với x,y<0
b. Phân tích thành nhân tử biểu thức: ab+b\(\sqrt{a}+\sqrt{a}+1\)(với a≥0)
a) Ta có: \(-7xy\cdot\sqrt{\dfrac{3}{xy}}\)
\(=\dfrac{-7xy\cdot\sqrt{3xy}}{xy}\)
\(=-7\sqrt{3}\cdot\sqrt{xy}\)
b) Ta có: \(ab+b\sqrt{a}+\sqrt{a}+1\)
\(=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)
Đúng 0
Bình luận (0)
$a)-7xy.\sqrt{\dfrac{3}{xy}}$
$=-7.\sqrt{x^2y^2.\dfrac{3}{xy}}(do \,x,y>0a\to xy>0)$
$=-7.\sqrt{\dfrac{xy}{3}}$
$b)ab+b\sqrt{a}+\sqrt{a}+1(a \ge 0)$
$=b\sqrt{a}(\sqrt{a}+1)+\sqrt{a}+1$
$=(\sqrt{a}+1)(b\sqrt{a}+1)$
Đúng 0
Bình luận (0)
a. Khử mẫu của biểu thức sau rồi rút gọn: -7xy.\(\sqrt{\dfrac{3}{xy}}\)với x,y<0
b. Phân tích thành nhân tử biểu thức: ab+\(b\sqrt{a}+\sqrt{a}+1\)(với a≥0)
a) \(-7xy.\sqrt{\dfrac{3}{xy}}=-7xy.\dfrac{\sqrt{3xy}}{xy}=-7\sqrt{3xy}\)
b) \(ab+b\sqrt{a}+\sqrt{a}+1=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)
Đúng 0
Bình luận (0)
a: \(-7xy\cdot\sqrt{\dfrac{3}{xy}}=-7xy\cdot\dfrac{\sqrt{3}}{\sqrt{xy}}=-7\sqrt{3xy}\)
b: \(ab+b\sqrt{a}+\sqrt{a}+1\)
\(=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)
Đúng 0
Bình luận (0)
rút gọn biểu thức: P=\(\dfrac{4\sqrt{xy}}{x-y}\):\(\left(\dfrac{1}{y-x}+\dfrac{1}{x+2\sqrt{x}\sqrt{y}+y^2}\right)\)-2x
\(P=\dfrac{4\sqrt{xy}}{x-y}:\left(\dfrac{1}{y-x}+\dfrac{1}{x+2\sqrt{x}\sqrt{y}+y}\right)-2x\) (với \(x\ne y,x,y\ge0\))
\(P=\dfrac{4\sqrt{xy}}{x-y}:\left(\dfrac{1}{\left(\sqrt{y}-\sqrt{x}\right)\left(\sqrt{y}+\sqrt{x}\right)}+\dfrac{1}{\left(\sqrt{x}+\sqrt{y}\right)^2}\right)-2x\)
\(P=\dfrac{4\sqrt{xy}}{x-y}:\left(\dfrac{\sqrt{y}+\sqrt{x}}{\left(\sqrt{y}+\sqrt{x}\right)^2\left(\sqrt{y}-\sqrt{x}\right)}+\dfrac{\sqrt{y}-\sqrt{x}}{\left(\sqrt{x}+\sqrt{y}\right)^2\left(\sqrt{y}-\sqrt{x}\right)}\right)-2x\)
\(P=\dfrac{4\sqrt{xy}}{x-y}:\left(\dfrac{\sqrt{y}+\sqrt{x}+\sqrt{y}-\sqrt{x}}{\left(\sqrt{y}-\sqrt{x}\right)\left(\sqrt{x}+\sqrt{y}\right)^2}\right)-2x\)
\(P=\dfrac{4\sqrt{xy}}{x-y}:\left(\dfrac{2\sqrt{y}}{\left(y-x\right)\left(\sqrt{x}+\sqrt{y}\right)}\right)-2x\)
\(P=\dfrac{4\sqrt{xy}}{x-y}\cdot\dfrac{\left(y-x\right)\left(\sqrt{x}+\sqrt{y}\right)}{2\sqrt{y}}-2x\)
\(P=\dfrac{4\sqrt{xy}\cdot\left(y-x\right)\left(\sqrt{x}+\sqrt{y}\right)}{\left(x-y\right)\cdot2\sqrt{y}}-2x\)
\(P=\dfrac{4\sqrt{xy}\cdot\left(y-x\right)\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\cdot2\sqrt{y}}-2x\)
\(P=\dfrac{2\sqrt{x}\left(y-x\right)}{\sqrt{x}-\sqrt{y}}-2x\)
\(P=\dfrac{2\sqrt{x}\left(y-x\right)-2x\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}\)
\(P=\dfrac{2y\sqrt{x}-2x\sqrt{x}-2x\sqrt{x}+2x\sqrt{y}}{\sqrt{x}-\sqrt{y}}\)
\(P=\dfrac{2y\sqrt{x}-4x\sqrt{x}+2x\sqrt{y}}{\sqrt{x}-\sqrt{y}}\)
Đúng 0
Bình luận (0)
Bài 1.Rút gọn A sqrt{x^2+dfrac{2x^2}{3}} với x0Bài 2.Rút gọn biểu thức left(dfrac{10+2sqrt{10}}{sqrt{5}+sqrt{2}}+dfrac{sqrt{30}-sqrt{6}}{sqrt{5}-1}right):dfrac{2}{2sqrt{5}-sqrt{6}}Bài 3.Cho ba biểu thức A asqrt{b} + bsqrt{a};B asqrt{a}-bsqrt{b} ;C a-b.Trong ba biểu thức trên biểu thức bằng biểu thức left(sqrt{a}-sqrt{b}right)left(sqrt{a}+sqrt{b}right) với a,b0Bài 7.Cho B dfrac{1}{sqrt{1}+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+dfrac{1}{sqrt{3}+sqrt{4}}+...+dfrac{1}{sqrt{98}+sqrt{99}}+dfrac{1}{sq...
Đọc tiếp
Bài 1.Rút gọn A = \(\sqrt{x^2+\dfrac{2x^2}{3}}\) với x<0
Bài 2.Rút gọn biểu thức \(\left(\dfrac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{30}-\sqrt{6}}{\sqrt{5}-1}\right)\):\(\dfrac{2}{2\sqrt{5}-\sqrt{6}}\)
Bài 3.Cho ba biểu thức A = a\(\sqrt{b}\) + b\(\sqrt{a}\);B = \(a\sqrt{a}-b\sqrt{b}\) ;C = a-b.Trong ba biểu thức trên biểu thức bằng biểu thức \(\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)\) với a,b>0
Bài 7.Cho B = \(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{98}+\sqrt{99}}+\dfrac{1}{\sqrt{99}+\sqrt{100}}\).Giá trị của biểu thức B là
Bài 8.Gọi M là giá trị nhỏ nhất của \(\dfrac{\sqrt{x}+1}{\sqrt{x}+4}\) và N là giá trị lớn nhất của \(\dfrac{\sqrt{x}+5}{\sqrt{x}+2}\).Tìm M và N
Giúp mình với!Mình đang cần gấp
1:
\(A=\sqrt{x^2+\dfrac{2x^2}{3}}=\sqrt{\dfrac{5x^2}{3}}=\left|\sqrt{\dfrac{5}{3}}x\right|=-x\sqrt{\dfrac{5}{3}}\)
2: \(=\left(\dfrac{\sqrt{100}+\sqrt{40}}{\sqrt{5}+\sqrt{2}}+\sqrt{6}\right)\cdot\dfrac{2\sqrt{5}-\sqrt{6}}{2}\)
\(=\dfrac{\left(2\sqrt{5}+\sqrt{6}\right)\left(2\sqrt{5}-\sqrt{6}\right)}{2}\)
\(=\dfrac{20-6}{2}=7\)
Đúng 0
Bình luận (0)