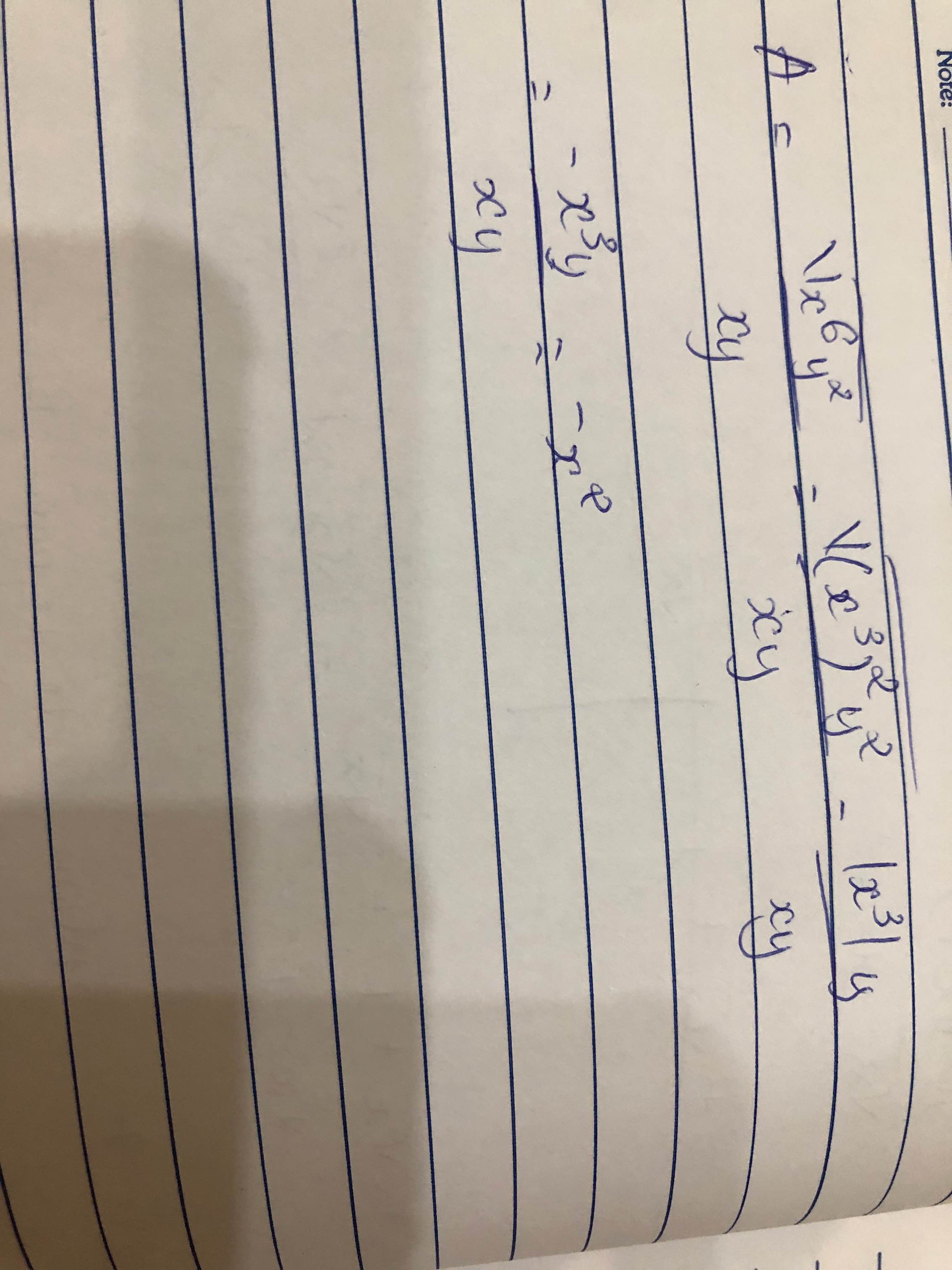\(\dfrac{\sqrt{x^6y^2}}{xy}=\dfrac{x^3y}{xy}=x^2\)
Bài 1: Căn bậc hai
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho niểu thức A dfrac{x+1}{sqrt{x}}+dfrac{xsqrt{x}-1}{x-sqrt{x}}+dfrac{x^2-xsqrt{x}+sqrt{x}-1}{sqrt{x}-xsqrt{x}} (Với x0, xne1)1) Rút gọn biểu thức A2) Chứng minh: Với x 0 và x ne1 thì A 33) Tìm các giá trị của x để biểu thức dfrac{6}{A}có giá trị là một số nguyên
Đọc tiếp
Cho niểu thức A= \(\dfrac{x+1}{\sqrt{x}}+\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}+\dfrac{x^2-x\sqrt{x}+\sqrt{x}-1}{\sqrt{x}-x\sqrt{x}}\)
(Với x>0, x\(\ne\)1)
1) Rút gọn biểu thức A
2) Chứng minh: Với x >0 và x \(\ne\)1 thì A >3
3) Tìm các giá trị của x để biểu thức \(\dfrac{6}{A}\)có giá trị là một số nguyên
A=(\(\dfrac{1}{\sqrt{x}+3}\)+\(\dfrac{\sqrt{x}+9}{x-9}\) ).\(\dfrac{\sqrt{x}}{2}\) ( (x≥0, x ≠0
a) rút gọn biểu thức
b)tìm giá trị nguyên của x để A có giá trị nguyên
Cho P= \(\dfrac{x^2+2xy+9y^2}{x+3x-2\sqrt{xy}}-2\sqrt{xy}\left(x,y>0\right)\) a, rút gọn P b, tìm điều kiện của x, y để biểu thức \(\dfrac{P}{\sqrt{xy}+y}\) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó
Rút gọn các biểu thức sau:
a, \(\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2\)
b, \(\sqrt{\dfrac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}}\) với \(x\ge1\)
1) rút gọn biểu thức sau :
a) dfrac{x+2sqrt{x}-3}{sqrt{x}-1} b) dfrac{4y+3sqrt{y}-7}{4sqrt{y}+7} c ) dfrac{xsqrt{y}-ysqrt{x}}{sqrt{x}-sqrt{y}}
d) dfrac{x-3sqrt{x}-4}{x-sqrt{x}-12} e) dfrac{1+sqrt{x}+sqrt{y}+sqrt{xy}}{1+sqrt{y}} ( với x0 , y0 )
f) sqrt{8-2sqrt{15}}+sqrt{5}+sqrt{3} g) sqrt{9-2sqrt{4}}-sqrt{9+2sqrt{14}}
Đọc tiếp
1) rút gọn biểu thức sau :
a) \(\dfrac{x+2\sqrt{x}-3}{\sqrt{x}-1}\) b) \(\dfrac{4y+3\sqrt{y}-7}{4\sqrt{y}+7}\) c ) \(\dfrac{x\sqrt{y}-y\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
d) \(\dfrac{x-3\sqrt{x}-4}{x-\sqrt{x}-12}\) e) \(\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{1+\sqrt{y}}\) ( với x>0 , y>0 )
f) \(\sqrt{8-2\sqrt{15}}+\sqrt{5}+\sqrt{3}\) g) \(\sqrt{9-2\sqrt{4}}-\sqrt{9+2\sqrt{14}}\)
\(\dfrac{2}{2+\sqrt{x}}\)+\(\dfrac{1}{2-\sqrt{x}}\)+\(\dfrac{2\sqrt{x}}{x-4}\)
rút gọn biểu thức
cho biểu thức A=\(\left(\dfrac{4x-9}{2\sqrt{x}-3}+\sqrt{x}\right)\cdot\dfrac{1}{x+2\sqrt{x}+1}\)
a)rút gọn
Cho biểu thức P=\(\dfrac{1}{x^2-\sqrt{x}}:\dfrac{\sqrt{x}+1}{x\sqrt{x}+x+\sqrt{x}}\)(với x >0 và x\(\ne1)\)
Rút gọn biểu thức P
Cho biểu thức P= \(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}-1}{x-1}\) với x ≥ 0, x ≠ 1)
a. Rút gọn P
b. CM: P < \(\dfrac{1}{3}\) với x ≥ 0, x ≠ 1