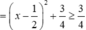\(A=x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=5^3-3.5.4=65\)

Bài 5

a) A = -x³ + 6x² - 12x + 8

= -x³ + 3.(-x)².2 - 3.x.2² + 2³

= (-x + 2)³

= (2 - x)³

Thay x = -28 vào A ta được:

A = [2 - (-28)]³

= 30³

= 27000

b) B = 8x³ + 12x² + 6x + 1

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³

= (2x + 1)³

Thay x = 1/2 vào B ta được:

B = (2.1/2 + 1)³

= 2³

= 8

Bài 6

a) 11³ - 1 = 11³ - 1³

= (11 - 1)(11² + 11.1 + 1²)

= 10.(121 + 11 + 1)

= 10.133

= 1330

b) Đặt B =  x³ - y³ = (x - y)(x² + xy + y²)

= (x - y)(x² - 2xy + y² + 3xy)

= (x - y)[(x - y)² + 3xy]

Thay x - y = 6 và xy = 9 vào B ta được:

B = 6.(6² + 3.9)

= 6.(36 + 27)

= 6.63

= 378

Bài 6 :

a) \(11^3-1=\left(11-1\right)\left(11^2+11+1^2\right)\)

\(\)\(=10.\left(121+12\right)\)

\(=10.133\)

\(=1330\)

b) \(\left\{{}\begin{matrix}x-y=6\\xy=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-2xy=36\\xy=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-2.18=36\\xy=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=72\\xy=9\end{matrix}\right.\)

Ta có :

\(x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)\)

\(=6.\left(72+9\right)\)

\(=6.81\)

\(=486\)

áp án B

Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9

⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11

⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1       *

 Nếu   x + 1 y + 1 > 9 ⇒ V T * > 0 ;   V P * < 0

Ngược lại nếu   x + 1 y + 1 < 9 ⇒ V T * < 0 ;   V P * > 0

Do đó   * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8

Khi đó   P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y

Đặt   t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t

⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29

a) \(A=x^3+y^3+3xy\)

\(=x^3+y^3+3xy\left(x+y\right)\) (do \(x+y=1\))

\(=x^3+3x^2y+3xy^2+y^3\)

\(=\left(x+y\right)^3\) \(=1\)

b) \(B=x^3-y^3-3xy\)

\(=x^3-y^3-3xy\left(x-y\right)\) (do \(x-y=1\))

\(=x^3-3x^2y+3xy^2-y^3\)

\(=\left(x-y\right)^3\) \(=1\)

Lời giải:

$M=x^3+y^3+2xy=(x+y)(x^2-xy+y^2)+2xy=x^2-xy+y^2+2xy$

$=x^2+y^2+xy=\frac{1}{4}(x-y)^2+\frac{3}{4}(x+y)^2=\frac{1}{4}(x-y)^2+\frac{3}{4}\geq \frac{3}{4}$

Vậy $M_{\min}=\frac{3}{4}$. Giá trị này đạt được khi $x=y=\frac{1}{2}$

Rút y=1-x có 

Chọn đáp án D.

a) \(11^3-1\)

\(=11^3-1^3\)

\(=\left(11-1\right)\left(11^2+11\cdot1+1^2\right)\)

\(=10\cdot\left(121+11+1\right)\)

\(=10\cdot\left(132+1\right)\)

\(=10\cdot133\)

\(=1330\)

b) Ta có:
\(x^3-y^3\)

\(=\left(x-y\right)^3+3xy\left(x-y\right)\)

Thay \(x-y=6\) và \(xy=20\) ta có:

\(6^3+3\cdot20\cdot6=216+60\cdot6=216+360=576\)

a: 11^3-1=(11-1)(11^2+11+1)

=10*(121+12)

=10*133=1330

b: x^3-y^3=(x-y)^3+3xy(x-y)

=6^3+3*20*6

=216+360

=576