đợi tý

a) Để \(A=\dfrac{2022}{\left|x\right|+2023}\) đạt Max thì |x| + 2023 phải đạt Min

Ta có \(\left|x\right|\ge0\forall x\Rightarrow\left|x\right|+2023\ge2023\forall x\)

\(\Rightarrow\dfrac{2022}{\left|x\right|+2023}\le\dfrac{2022}{2023}\forall x\)

Dấu "=" xảy ra khi \(\left|x\right|=0\Rightarrow x=0\)

Vậy Max \(A=\dfrac{2022}{\left|x\right|+2023}=\dfrac{2022}{2023}\) đạt được khi x = 0

b) Để \(B=\left(\sqrt{x}+1\right)^{99}+2022\) đạt Min với \(x\ge0\) thì \(\sqrt{x}+1\) phải đạt Min

Ta có \(\sqrt{x}\ge0\forall x\ge0\Rightarrow\sqrt{x}+1\ge1\forall x\ge0\)

\(\Rightarrow\left(\sqrt{x}+1\right)^{99}+2022\ge1+2022\ge2023\forall x\ge0\)

Dấu "=" xảy ra khi \(\sqrt{x}=0\Rightarrow x=0\)

Vậy Max \(B=\left(\sqrt{x}+1\right)^{99}+2022=2023\) đạt được khi x = 0

Câu c) và d) thì tự làm, ko có rảnh =))))

Đã trả lời rồi còn độ tí đồ ngull

                      Bài làm :

Ta có :

\(\left(a+b\right)^2\ge4ab\)

\(\Leftrightarrow\frac{a+b}{ab}\ge\frac{4}{a+b}\)

\(\Leftrightarrow\frac{4}{a+b}\le\frac{1}{a}+\frac{1}{b}\)

\(\Leftrightarrow\frac{1}{a+b}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\left(1\right)\)

Dấu "=" xảy ra khi : a=b

Chứng minh tương tự như trên ; ta có :

\(\hept{\begin{cases}\frac{1}{b+c}\text{≤}\frac{1}{4}\left(\frac{1}{b}+\frac{1}{c}\right)\left(2\right)\\\frac{1}{c+a}\text{≤}\frac{1}{4}\left(\frac{1}{c}+\frac{1}{a}\right)\left(3\right)\end{cases}}\)

Cộng vế với vế của (1) ; (2) ; (3) ; ta được :

\(A\text{≤}\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\text{=}\frac{3}{2}\)

Dấu "=" xảy ra khi ;

\(\hept{\begin{cases}a=b=c\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\end{cases}}\Leftrightarrow a=b=c=1\)

Vậy Max (A) = 3/2 khi a=b=c=1

quản lí tên kiểu j z

aaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffffaaaaaaaaaaaaaaaaaaaaaaffffffffffffffffffffffffffff

Áp dụng bất đẳng thức: \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)

\(\Leftrightarrow\left(a+b\right)^2\ge4ab\) \(\Leftrightarrow a^2+2ab+b^2\ge4ab\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow\left(a-b\right)^2\ge0\left(đúng\right)\)

\(\dfrac{1}{2a+b+c}=\dfrac{1}{4}.\dfrac{4}{2a+b+c}\le\dfrac{1}{4}\left(\dfrac{1}{2a}+\dfrac{1}{b+c}\right)\le\dfrac{1}{4}\left[\dfrac{1}{2a}+\dfrac{1}{4}\left(\dfrac{1}{b}+\dfrac{1}{c}\right)\right]=\dfrac{1}{8}\left(\dfrac{1}{a}+\dfrac{1}{2b}+\dfrac{1}{2c}\right)\)

CMTT \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{a+2b+c}\le\dfrac{1}{8}\left(\dfrac{1}{2a}+\dfrac{1}{b}+\dfrac{1}{2c}\right)\\\dfrac{1}{a+b+2c}\le\dfrac{1}{8}\left(\dfrac{1}{2a}+\dfrac{1}{2b}+\dfrac{1}{c}\right)\end{matrix}\right.\)

\(\Rightarrow M=\dfrac{1}{2a+b+c}+\dfrac{1}{a+2b+c}+\dfrac{1}{a+b+2c}\le\dfrac{1}{8}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{2}{2a}+\dfrac{2}{2b}+\dfrac{2}{2c}\right)=\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{4}.4=1\)

\(minM=1\Leftrightarrow a=b=c=\dfrac{3}{4}\)

Thỏa mãn $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$ hay $a+b+c=1$ vậy bạn?

cái cuối là \(\dfrac{1}{\sqrt{c^2-ca+a^2}}\)  nha

\(a^2+b^2-ab\ge\dfrac{1}{2}\left(a+b\right)^2-\dfrac{1}{4}\left(a+b\right)^2=\dfrac{1}{4}\left(a+b\right)^2\)

\(\Rightarrow\dfrac{1}{\sqrt{a^2-ab+b^2}}\le\dfrac{1}{\sqrt{\dfrac{1}{4}\left(a+b\right)^2}}=\dfrac{2}{a+b}\le\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)

Tương tự:

\(\dfrac{1}{\sqrt{b^2-bc+c^2}}\le\dfrac{1}{2}\left(\dfrac{1}{b}+\dfrac{1}{c}\right)\) ; \(\dfrac{1}{\sqrt{c^2-ca+a^2}}\le\dfrac{1}{2}\left(\dfrac{1}{c}+\dfrac{1}{a}\right)\)

Cộng vế:

\(P\le\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)

Dấu "=" xảy ra khi \(a=b=c=1\)

Ai lm đc câu nào thì giúp mk với , cảm ơn !!

\(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\\ A_{min}=\dfrac{1}{9}\Leftrightarrow x=\dfrac{3}{5}\\ B=\dfrac{2009}{2008}-\left|x-\dfrac{3}{5}\right|\le\dfrac{2009}{2008}\\ B_{max}=\dfrac{2009}{2008}\Leftrightarrow x=\dfrac{3}{5}\\ C=-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\le1\dfrac{2}{3}\\ C_{max}=1\dfrac{2}{3}\Leftrightarrow\dfrac{1}{3}x=-4\Leftrightarrow x=-12\)

a: \(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{3}{5}\)

Bài 1: Ta có:

\(M=\frac{ad}{abcd+abd+ad+d}+\frac{bad}{bcd.ad+bc.ad+bad+ad}+\frac{c.abd}{cda.abd+cd.abd+cabd+abd}+\frac{d}{dab+da+d+1}\)

\(=\frac{ad}{1+abd+ad+d}+\frac{bad}{d+1+bad+ad}+\frac{1}{ad+d+1+abd}+\frac{d}{dab+da+d+1}\)

$=\frac{ad+abd+1+d}{ad+abd+1+d}=1$

Bài 2:

Vì $a,b,c,d\in [0;1]$ nên

\(N\leq \frac{a}{abcd+1}+\frac{b}{abcd+1}+\frac{c}{abcd+1}+\frac{d}{abcd+1}=\frac{a+b+c+d}{abcd+1}\)

Ta cũng có:
$(a-1)(b-1)\geq 0\Rightarrow a+b\leq ab+1$

Tương tự:

$c+d\leq cd+1$

$(ab-1)(cd-1)\geq 0\Rightarrow ab+cd\leq abcd+1$

Cộng 3 BĐT trên lại và thu gọn thì $a+b+c+d\leq abcd+3$

$\Rightarrow N\leq \frac{abcd+3}{abcd+1}=\frac{3(abcd+1)-2abcd}{abcd+1}$

$=3-\frac{2abcd}{abcd+1}\leq 3$

Vậy $N_{\max}=3$

3.

Hình vẽ:

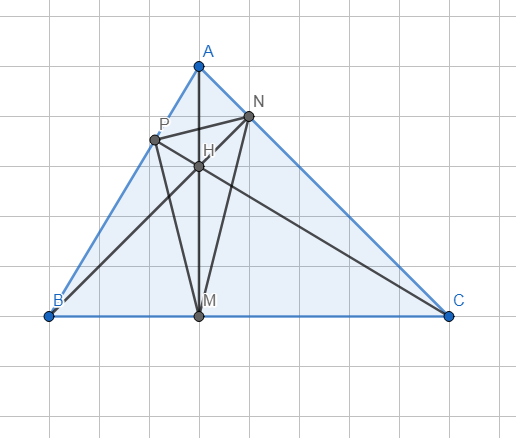
Lời giải:

a) △AMC và △BNC có: \(\widehat{AMC}=\widehat{BNC}=90^0;\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△AMC∼△BNC (g-g).

\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CM}{CN}\Rightarrow AC.CN=BC.CM\left(1\right)\)

b) △AMB và △CPB có: \(\widehat{AMB}=\widehat{CPB}=90^0;\widehat{ABC}\) là góc chung.

\(\Rightarrow\)△AMB∼△CPB (g-g)

\(\Rightarrow\dfrac{AB}{CB}=\dfrac{BM}{BP}\Rightarrow AB.BP=BC.BM\left(2\right)\)

Từ (1) và (2) suy ra:

\(AC.CN+AB.BP=BC.CM+BC.BM=BC.\left(CM+BM\right)=BC.BC=BC^2\left(đpcm\right)\)b) Gọi \(M_0\) là trung điểm BC, giả sử \(AB< AC\).

\(\widehat{HBM}=90^0-\widehat{BHM}=90^0-\widehat{AHN}=\widehat{CAM}\)

△HBM và △CAM có: \(\widehat{HBM}=\widehat{CAM};\widehat{HMB}=\widehat{CMA}=90^0\)

\(\Rightarrow\)△HBM∼△CAM (g-g) 

\(\Rightarrow\dfrac{MH}{CM}=\dfrac{BM}{MA}\Rightarrow MH.MA=BM.CM\)

Ta có: \(BM.CM=\left(BM_0-MM_0\right)\left(CM_0+MM_0\right)=\left(BM_0-MM_0\right)\left(BM_0+MM_0\right)=BM_0^2-MM_0^2\le BM_0^2=\dfrac{BC^2}{4}\)

\(\Rightarrow MH.MA\le\dfrac{BC^2}{4}\).

Vì \(BC\) không đổi nên: \(max\left(MH.MA\right)=\dfrac{BC^2}{4}\), đạt được khi △ABC cân tại A hay A nằm trên đường trung trực của BC.

c) Sửa đề: \(S_1.S_2.S_3\le\dfrac{1}{64}.S^3\)

△AMC∼△BNC \(\Rightarrow\dfrac{AC}{BC}=\dfrac{MC}{NC}\Rightarrow\dfrac{AC}{MC}=\dfrac{BC}{NC}\)

△ABC và △MNC có: \(\dfrac{AC}{MC}=\dfrac{BC}{NC};\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△ABC∼△MNC (c-g-c)

\(\Rightarrow\dfrac{S_{MNC}}{S_{ABC}}=\dfrac{S_1}{S}=\dfrac{MC}{AC}.\dfrac{NC}{BC}\left(1\right)\)

Tương tự: 

△ABC∼△MBP \(\Rightarrow\dfrac{S_{MBP}}{S_{ABC}}=\dfrac{S_2}{S}=\dfrac{MB}{AB}.\dfrac{BP}{BC}\left(2\right)\)

△ABC∼△ANP \(\Rightarrow\dfrac{S_{ANP}}{S_{ABC}}=\dfrac{S_3}{S}=\dfrac{AN}{AB}.\dfrac{AP}{AC}\left(3\right)\)

Từ (1), (2), (3) suy ra:

\(\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}=\left(\dfrac{MC}{AC}.\dfrac{NC}{BC}\right).\left(\dfrac{MB}{AB}.\dfrac{BP}{BC}\right).\left(\dfrac{AN}{AB}.\dfrac{AP}{AC}\right)\) 

\(\Rightarrow\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}=\left(\dfrac{MC.MB}{AC.AB}\right).\left(\dfrac{BP.AP}{AC.BC}\right).\left(\dfrac{AN.CN}{AB.BC}\right)\) (*)

Áp dụng câu b) ta có:

\(\left\{{}\begin{matrix}BM.CM\le\dfrac{1}{4}BC^2\\AP.BP\le\dfrac{1}{4}AB^2\\AN.CN\le\dfrac{1}{4}AC^2\end{matrix}\right.\)

Từ (*) suy ra:

\(\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}\le\left(\dfrac{\dfrac{1}{4}BC^2}{AC.AB}\right).\left(\dfrac{\dfrac{1}{4}AC^2}{AC.BC}\right).\left(\dfrac{\dfrac{1}{4}AB^2}{AB.BC}\right)=\dfrac{1}{64}\)

\(\Rightarrow S_1.S_2.S_3\le\dfrac{1}{64}.S^3\)

Dấu "=" xảy ra khi △ABC đều.

a: \(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}=\dfrac{-3\sqrt{x}-9}{x-9}\)

\(=\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3}{\sqrt{x}-3}\)

b: A=1/3

=>\(\dfrac{-3}{\sqrt{x}-3}=\dfrac{1}{3}\)

=>căn x-3=-9

=>căn x=-6(loại)

c: căn x-3>=-3

=>3/căn x-3<=-1

=>-3/căn x-3>=1

Dấu = xảy ra khi x=0

ĐKXĐ : \(x\ne0;x\ne\pm1\)

a) Bạn ghi lại rõ đề.

b) \(B=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{x^2-1}=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{\left(x-1\right).\left(x+1\right)}\)

\(=\dfrac{\left(x-1\right)^2+3x-x^2}{\left(x-1\right).\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right).\left(x+1\right)}=\dfrac{1}{x-1}\)

c) \(P=A.B=\dfrac{x^2+x-2}{x.\left(x-1\right)}=\dfrac{\left(x-1\right).\left(x+2\right)}{x\left(x-1\right)}=\dfrac{x+2}{x}=1+\dfrac{2}{x}\)

Không tồn tại Min P \(\forall x\inℝ\)