Cho tam giác ABC nội tiếp (O), có đường cao AD, H là trực tâm. (O;OH) cắt AH tại E( khác F). F đối xứng với E qua BC. Gọi N là trung điểm của HE. C/m: AH=2DN

Những câu hỏi liên quan
cho tam giác abc nội tiếp đường tròn tâm O. BE,CF là 2 đường cao H là trực tâm AD là đường kính H cắt đường tròn tâm O tại P. Chứng minh PD song song BC, BAP=CAD
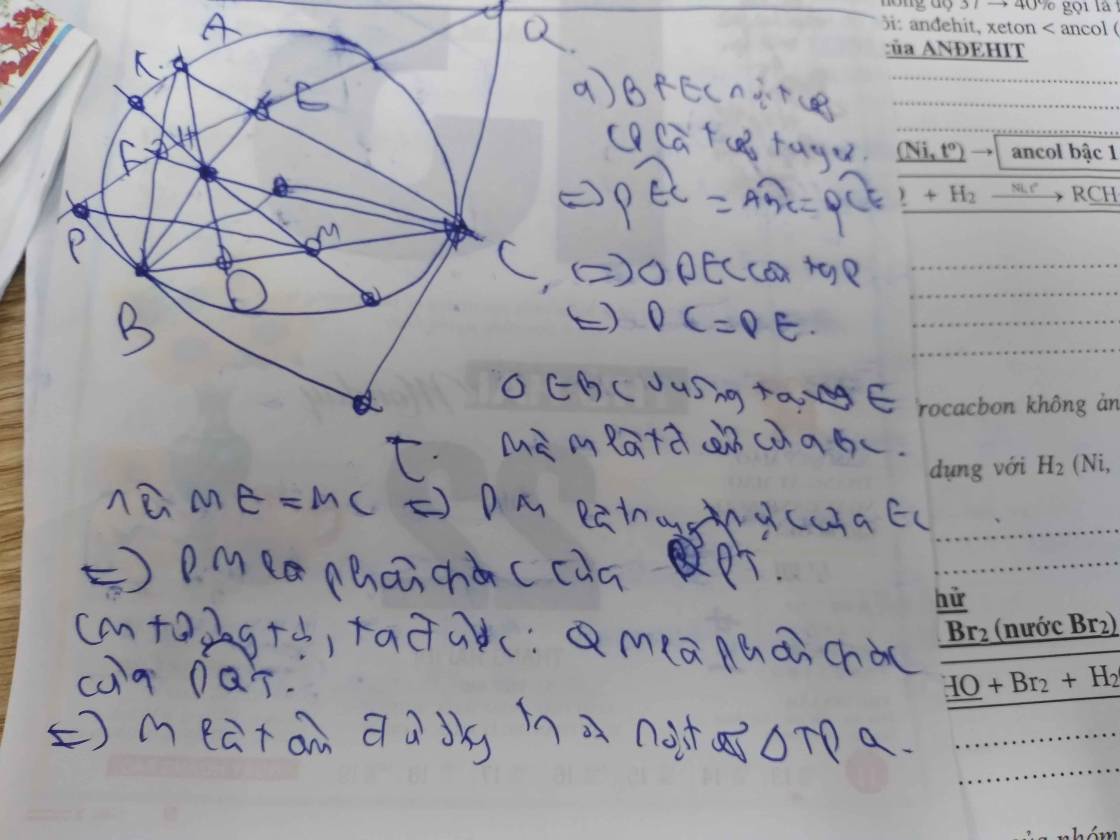
Bài 11: Cho tam giác ABC nội tiếp (O), đường cao AD, BE, CF, trực tâm H, M là trung điểm BC. Tia MH cắt (O) tại K. Tiếp tuyến tại B, C của (O) cắt nhau tại T.TB, TC cắt EF tại P, Q.a) Chứng minh M là tâm nội tiếp tam giác TPQ.KEDMTb) Chứng minh: M,B, P, K, E đồng viên. c) Chứng minh: KP, CF cắt nhau trên (O). d) Chứng minh: TPKQ nội tiếp (J). e) Chứng minh (J) tiếp xúc (O).
Cho tam giác ABC nội tiếp đường tròn (O) có đường cao AD, BE, CF và trực tâm H. Gọi k là giao điểm của AH và đường tròn (O). Chứng minh rằng DH=DK
tam giác abc nhọn nội tiếp (o), h là trực tâm tam giác abc, đg cao ad,be,cf, m là trung điểm bc. cm dmef nội tiếp
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Các đường cao AD; BE; CF của tam giác ABC cùng đi qua trực tâm H. 1) Chứng minh tứ giác BFEC nội tiếp; 2) Kẻ đường kính AK của đường tròn (O). Chứng minh tam giác ABD đồng dạng với tam giác AKC và AB.AC 2. AD. R; 3) Gọi M là hình chiếu vuông góc của C trên AK. Chứng minh rằng MD song song với BK. 4) Giả sử BC là dây cố định của đường tròn (O) còn A di động trên cung lớn BC. Tìm vị trí điểm A để diện tích tam giác AEH lớn nhất.
Đọc tiếp
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Các đường cao AD; BE; CF của tam giác
ABC cùng đi qua trực tâm H.
1) Chứng minh tứ giác BFEC nội tiếp;
2) Kẻ đường kính AK của đường tròn (O). Chứng minh tam giác ABD đồng dạng với tam giác
AKC và AB.AC = 2. AD. R;
3) Gọi M là hình chiếu vuông góc của C trên AK. Chứng minh rằng MD song song với BK.
4) Giả sử BC là dây cố định của đường tròn (O) còn A di động trên cung lớn BC. Tìm vị trí
điểm A để diện tích tam giác AEH lớn nhất.
CHO tam giác ABC có 3 góc nhọn (AB<AC) NỘI TIẾP tam giác đường tròn (o) gọi H là trực tâm và M, N, P lần lượt là chân đường cao kẻ từ các đỉnh A, B, C của tam giác ABC.
a) CM:các tứ giác APHN và BPNC nội tiếp
b) CM; H LÀ tâm đường tròn nội tiếp tam giác MNP
VẼ hình hộ mk vs ạ![]()
Cho tam giác ABC nhọn nội tiếp (O;R). Có các đường cao AD,BE,CF, H là trực tâm tam giác ABC. Kẻ đường kính AK.
c) Khi BC và (O) cố định , BC=a. Tìm vị trí của A để P= DE+EF+DF lớn nhất, tìm GTLN theo a và R
cho tam giác ABC nhọn có ABAC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC2R.AD2. chứng minh HK đi qua tring điểm M của BC3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2R^2-r^24. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Đọc tiếp
cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N
1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC=2R.AD
2. chứng minh HK đi qua tring điểm M của BC
3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2=R^2-r^2
4. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Cho tam giác ABC nội tiếp (O), đường cao AD, BE, CF, trực tâm H. AH cắt (O) tại K. Chứng minh: DH=DK.
Mọi người ơi em cần rất gấp ạ
Lời giải:
$\widehat{HBD}=\widehat{EBC}=\widehat{CAD}$ (cùng phụ góc $\widehat{ACB}$)
$\widehat{CAD}=\widehat{CAK}=\widehat{KBC}=\widehat{KBD}$ (góc nt chắn cung $CK$)
$\Rightarrow \widehat{HBD}=\widehat{KBD}$
Xét tam giác vuông tại $D$ là $HBD$ và $KBD$ có:
$\widehat{HBD}=\widehat{KBD}$ (cmt)
$BD$ chung
$\Rightarrow \triangle HBD=\triangle KBD$ (g.c.g)
$\Rightarrow HD=KD$ (đpcm)
Đúng 1
Bình luận (1)