Cho tam giác ABC có AB = AC, kẻ \(BD\perp AC;CE\perp AB\). Gọi O là giao điểm. Chứng minh:
a) BD = CE
b) AO là tia phân giác góc BEC
c) \(\Delta OBE=\Delta OCD\)
Cho tam giác ABC có AB = AC, từ điểm B kẻ \(BE\perp\) AC tại E, từ điểm C kẻ CD \(\perp\) AD tại D.
a) Chứng minh BD = CE
b) Đoạn BD cắt đoạn BE tại O.Chứng minh tam giác OBD = tam giác OCE
c) Chứng minh DE // BC
#\(N\)
*Sửa đề: `CD \bot AB` chứ không phải `AD, BE` cắt đoạn `CD` tại `O` chứ không phải đoạn `BD.`
`a,` Vì Tam giác `ABC` có `AB = AC ->`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `BDC` và Tam giác `CEB` có:
`BC` chung
\(\widehat{B}=\widehat{C}\) `(CMT)`
\(\widehat{BDC}=\widehat{CEB}=90^0\)
`=>` Tam giác `BDC =` Tam giác `CEB (ch-gn)`
`-> BD = CE (2` cạnh tương ứng `)`
`b,` Xét Tam giác `ADC` và Tam giác `AEB` có:
`AB = AC (g``t)`
\(\widehat{A}\) chung
\(\widehat{AEB}=\widehat{ADC}=90^0\)
`=>` Tam giác `ADC =` Tam giác `AEB (ch-gn)`
`=>` \(\widehat{ABE}=\widehat{ACD}\) `( 2` góc tương ứng `)`
Xét Tam giác `OBD` và Tam giác `OCE` có:
\(\widehat{ODB}=\widehat{OEC}=90^0\)
`BD = CE (CMT)`
\(\widehat{DBO}=\widehat{ECO}\) `(CMT)`
`=>` Tam giác `OBD =` Tam giác `OCE (g-c-g)`
`c,` *Mình sẽ bổ sung sau nha bạn .-. câu này mình bị bí á .-.
lm nốt câu c nha=))
c:
Có `Delta OBD=Delta OCE(cmt)`
`=>OD=OE` ( `2` cạnh tương ứng )
Có `CD ⊥ AB(GT)=>hat(ADC)=90^0=>hat(ADO)=90^0`
`BE⊥AC(GT)=>hat(AEB)=90^0=>hat(AEO)=90^0`
Xét `Delta ADO` và `Delta AEO` có :
`hat(ADO)=hat(AEO)(=90^0)`
`AO` -chung
`DO=EO(cmt)`
`=>Delta ADO=Delta AEO(c.h-c.g.v)`
`=>AD=AE` ( hai cạnh tương ứng )
`=>Delta ADE` cân tại `A=>hat(ADE)=(180^0-hat(A))/2`
`Delta ABC` cân tại `A(AB=AC)=>hat(ABC)=(180^0-hat(A))/2`
nên `hat(ADE)=hat(ABC)`
mà `2` góc này ở vị trí đvị
nên `DE////BC`(đpcm)
hình :
Cho tam giác ABC có AB=AC kẻ AH vuông góc với BC (H thuộc BC)
a,Chứng minh :HB=HC
b,Kẻ HD\(\perp\)AB(D\(\in\)AB),HE\(\perp\)AC(E\(\in\)AC):Chứng minh HD=HE
c,Chứng minh BD=BC
PLS Help me!!!!
a) ta có AH⊥BC \(\Rightarrow\)\(\widehat{AHB}=\widehat{AHC}\)=90 độ
ta có AB=AC \(\Rightarrow\)\(\Delta\)ABC cân tại A
\(\Rightarrow\)\(\widehat{ABC}\)=\(\widehat{ACB}\) hay\(\widehat{ABH}=\widehat{ACH}\)
Xét \(\Delta\)AHB\(\left(\widehat{AHB}=90độ\right)\) và \(\Delta\)AHC \(\left(\widehat{AHC}=90\right)độ\) có
AB=AC(giả thiết)
\(\widehat{ABH}=\widehat{ACH}\) (chứng minh trên)
\(\Rightarrow\) \(\Delta\)AHB= \(\Delta\)AHC(cạnh huyền - góc nhọn)
\(\Rightarrow\)HB=HC(2 góc tương ứng)
vậy HB=HC
b) \(\Delta\)AHB= \(\Delta\)AHC(chứng minh câu a)
\(\Rightarrow\widehat{HAB}=\widehat{HAC}\) hay \(\widehat{HAD}=\widehat{HAE}\)
ta có HD⊥AB \(\Rightarrow\widehat{HDA}=90độ\)
HE⊥AC \(\Rightarrow\widehat{HEA}=90độ\)
Xét \(\Delta\)AHD (\(\widehat{HDA}=90độ\)) và \(\Delta\)AHE \(\left(\widehat{HEA}=90\right)độ\) có
\(\widehat{HAD}=\widehat{HAE}\) (chứng minh trên )
AH là cạnh huyền chung
\(\Rightarrow\)\(\Delta\)AHD = \(\Delta\)AHE (cạnh huyền -góc nhọn)
\(\Rightarrow HD=HE\) ( 2 góc tương ứng)
vậy HD=HE
c) ta có HD⊥AB \(\Rightarrow\widehat{HDB}=90độ\)
HE⊥AC \(\Rightarrow\widehat{HEC}=90độ\)
\(\Delta\)ABC cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\) hay \(\widehat{DBH}=\widehat{ECH}\)
Xét \(\Delta\)HDB\(\left(\widehat{HDB}=90độ\right)\) và \(\Delta\)HEC \(\left(\widehat{HEC}=90độ\right)\)
BH=HC (chứng minh câu a)
\(\widehat{DBH}=\widehat{ECH}\) (chứng minh trên)
\(\Rightarrow\Delta HDB=\Delta HEC\) (cạnh huyền -góc nhọn)
\(\Rightarrow BD=EC\) (2 cạnh tương ứng )
vậy BD =EC
Bài 5: Cho tam giác ABC có AB=AC, Kẻ BD\(\perp\)AC tại D, Kẻ CE\(\perp\)AB tại E, BD cắt CE tại H
a) Chứng minh: \(\Delta\)ABD = \(\Delta\)ACE
b) Chứng minh: \(\Delta\)BCD = \(\Delta\)CBE
c) Chứng minh: \(\Delta\)BCD = \(\Delta\)CHD
d) Chứng minh: AH là tia phân giác của góc BAC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên BD=CE; AD=AE
Xét ΔBCD và ΔCBE có
BC chung
CD=BE
BD=CE
DO đó: ΔBCD=ΔCBE
c: Xét ΔBHE vuông tại E và ΔCHD vuông tại D có
BE=CD
\(\widehat{EBH}=\widehat{DCH}\)
Do đó: ΔBHE=ΔCHD
d: Ta có: ΔBHE=ΔCHD
nên HB=HC
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
Cho tam giác ABC có AB = 10cm, BC = 16cm. Kẻ phân giác BD \(\left(D\in AC\right)\), kẻ \(AH\perp BD\). Gọi M là trung điểm AC. Tính HM
Cho tam giác ABC vuông tại A , phân giác AD , biết AB = 6, AC = 8
a, Tính BD, CD
b, Qua B kẻ đường thẳng song song với AD, cắt AC tại E.. Tính AE
c, Kẻ DI \(\perp\)AC , I \(\in\) AC. CMR : \(\dfrac{CI}{IA}=\dfrac{AC}{AB}\)
Bài 2:
\(2\left(x^2+\dfrac{1}{x^2}\right)-x-\dfrac{1}{x}=6\dfrac{ }{ }\)
Bài 2:ĐKXĐ: x<>0
\(2\left(x^2+\frac{1}{x^2}\right)-x-\frac{1}{x}=6\)
=>\(2\left\lbrack\left(x+\frac{1}{x}\right)^2-2\cdot x\cdot\frac{1}{x}\right\rbrack-\left(x+\frac{1}{x}\right)=6\)
=>\(2\left(x+\frac{1}{x}\right)^2-4-\left(x+\frac{1}{x}\right)-6=0\)
=>\(2\left(x+\frac{1}{x}\right)^2-\left(x+\frac{1}{x}\right)-10=0\)
=>\(2\left(x+\frac{1}{x}\right)^2-5\left(x+\frac{1}{x}\right)+4\left(x+\frac{1}{x}\right)-10=0\)
=>\(\left(x+\frac{1}{x}\right)\left\lbrack2\left(x+\frac{1}{x}\right)-5\right\rbrack+2\cdot\left\lbrack2\left(x+\frac{1}{x}\right)-5\right\rbrack=0\)
=>\(\left(x+\frac{1}{x}+2\right)\left(2x+\frac{2}{x}-5\right)=0\)
=>\(\frac{x^2+2x+1}{x}\cdot\frac{2x^2-5x+2}{x}=0\)
=>\(\left(x+1\right)^2\left(2x^2-5x+2\right)=0\)
=>\(\left(x+1\right)^2\cdot\left(x-2\right)\left(2x-1\right)=0\)
=>\(\left[\begin{array}{l}x+1=0\\ x-2=0\\ 2x-1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-1\left(nhận\right)\\ x=2\left(nhận\right)\\ x=\frac12\left(nhận\right)\end{array}\right.\)
Bài 1:
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10
Xét ΔABC có AD là phân giác
nên \(\frac{BD}{AB}=\frac{CD}{AC}\)
=>\(\frac{BD}{6}=\frac{CD}{8}\)
mà BD+CD=BC=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{BD}{6}=\frac{CD}{8}=\frac{BD+CD}{6+8}=\frac{10}{14}=\frac57\)
=>\(\begin{cases}BD=6\cdot\frac57=\frac{30}{7}\\ CD=8\cdot\frac57=\frac{40}{7}\end{cases}\)
b: Xét ΔCEB có AD//EB
nên \(\frac{CA}{AE}=\frac{CD}{DB}\)
=>\(\frac{8}{AE}=\frac43=\frac86\)
=>AE=6(cm)
c: Ta có: DI⊥AC
AB⊥CA
Do đó: DI//AB
Xét ΔCAB có DI//AB
nên \(\frac{CI}{IA}=\frac{CD}{DB}\)
=>\(\frac{CI}{IA}=\frac{CA}{AB}\)
Cho tam giác ABC có AB<AC. Kẻ \(BD\perp AC\), \(CE\perp AB\)
Cm: BD<CE
Bài 4:Cho tam giác ABC có CA = CB = 10cm, AB = 12cm. Kẻ CI \(\perp\) AB (I ϵ AB). Kẻ IH \(\perp\) AC (H ϵ AC), IK \(\perp\) BC (K ϵ BC)
a, Chứng minh rằng IA = IB
b, Chứng minh rằng IH = IK
c, Tính độ dài IC
d, HK // AB
a: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CA=CB
CI chung
Do đó: ΔCIA=ΔCIB
Suy ra: IA=IB
b: Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó: ΔCHI=ΔCKI
Suy ra: IH=IK
c: IA=IB=AB/2=6(cm)
nen IC=8(cm)
d: Xét ΔCAB có CH/CA=CK/CB
nên HK//AB
Cho tam giác ABC có AB = AC, lấy D \(\in\) AC, E \(\in\) AB sao cho \(\widehat{ADB}=\widehat{AEC}\). BD cắt CE tại I. Chứng minh:
a. BD = CE
b. tam giác EIB = tam giác DIC
c. AI là tia phân giác của \(\widehat{BAC}\)
d. AI \(\perp\)BC
e. DE // BC
Các bạn vẽ hình và giải giúp mik nhé!
a )ta có góc ADB =góc AEC
mà góc A là góc chung
=>góc ECA=góc DBA
Xét △ADB và △AEC có
góc A là góc chung
góc ABD=góc ACE
AB=AC(giả thiết )
=> △ADB=△AEC(g-c-g)
=>BD=CE
vậy BD =CE
b)ta có góc AEC+góc BEC =180 độ
góc ADB +góc CDB =180 độ
mà góc AEC=góc ADB (giả thiết)
=>góc BEC =góc CDB hay góc BEI =góc CDI
ta có △ADB =△AEC(chứng minh câu a)
=>AD=AE
mà AB=AC( giả thiết)
=>BE =DC
xét △BEI và △CDI có
góc BEI =góc CDI (chứng minh trên)
góc EIB=góc DIC(2 góc đối đỉnh)
=>góc EBI =góc DCI hay góc ABI=góc ACI
Xét △EBI và △DCI có
góc EBI =góc DCI(chứng minh trên)
góc BEI =góc CDI(chứng minh trên)
BE=DC(chứng minh trên )
=>△EBI = △DCI (g-c-g)
vậy △EBI = △DCI
c)ta có △EBI = △DCI(chứng minh câu b)
=>BI =IC
Xét △AIB và △AIC có
AB=AC(giả thiết )
góc ABI =ACI(chứng minh câu b)
BI =CI(chứng minh trên )
=> △AIB = △AIC(c-g-c)
=>góc BAI =góc CAI
vây AI là tia phân giác của góc BAC
d) kéo dài AI cắt BC tại F;ta có góc BAI=góc CAI(chứng minh câu b)hay góc BAD=góc CAD
ta có AB =AC => △ABC cân tại A=> góc B=góc C
Xét △BADvà △CAD có
AB=AC(giả thiết )
góc BAD =góc CAD
AI là cạnh chung
=>△BAD=△CAD(c-g-c)
=>góc AIB=gócAIC
mà góc AIB+gócAIC =180 độ
=> góc AIB =góc AIC =\(\dfrac{180độ}{2}\)=90 độ
vậy AI ⊥BC
e)ta có △ABC cân tại A =>góc ACB =\(\dfrac{180-gócA}{2}\)
ta có AD=AE (chứng minh câu b) => △AED cân tại A
=> góc ADE=\(\dfrac{180-\text{góc A}}{2}\)
=> góc ACB =góc ADE mà 2 góc này là 2 góc đồng vị của đường thẳng CA cắt ED và BC => ED//BC
vậy ED//BC
nhớ tim nha
Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm. Đường phân giác AD. Kẻ \(DE\perp AB;DF\perp AC\). Qua đỉnh A của tam giác ABC kẻ đường thẳng d không song song với BC, đường thẳng này cắt DE, DF kéo dài tại M, N. Chứng minh BM // CN
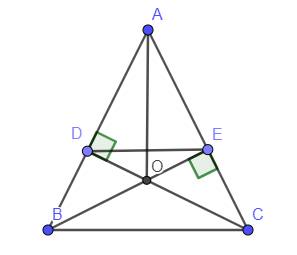
Cho tam giác ABC ( góc A<90 độ), AB = AC. Kẻ \(BD\perp AC\)tại D; \(CE\perp AB\)tại E. O là giao điểm củ BD và CE. Chứng minh \(OA\perp BC\)và ED
Ghi cách giải giúp mình luôn nhé!!