cho tam giác ABC có AM vuông góc BM; AN vuông góc BN, B1= B2=\(\dfrac{1}{2}\) ABC. Chứng minh: tam giác MAB đồng dạng tam giác ABC

Những câu hỏi liên quan
cho tam giác abc, kẻ BM vuông góc với AC tại M, biết Bm = 8cm, AB = 10 cm, MC = 15cm. Tính BC và AM. Hỏi tam giác ABC có vuông không? vì sao
xét tam giác BAM vuông tại M => Bm^2+ AM^2=AB^2 (định lý pytago)
=> 8^2+Am^2=10^2 => AM^2=36=6^2
xét tam giác BMC vuông tại M => BM^2 +MC^2 = BC^2
=> 8^2 + 15^2 =BC^2
=> BC^2= 17^2
=> AC=21 . tam giác abc: AB^2+BC^2ko bằng AC^2
=> tam giác abc ko vuông
Đúng 1
Bình luận (0)
Cho tam giác vuông tại A,có BM là tia phân giác của góc ABC(M thuộc AC).Kẻ MH vuông góc BC(H thuộc BC)
a)chứng minh tam giác AMB=tam giác HBM
b)chứng minh AM=HM
C)so sánh AM và MC
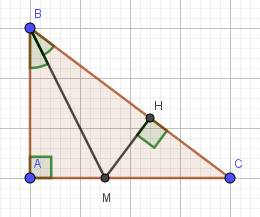
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
Đúng 2
Bình luận (0)
Cho Tam giác ABC vuông tại A, BM là tia phân giác. Vẽ MH vuông góc BC, MH cắt AB tại e
a) chứng minh tam giác ABM = tam giác HBM
b)so sánh AM và CM
c)chứng minh BM vuông góc EC
a: Xét ΔABM vuông tại A và ΔHBM vuông tại H có
BM chung
\(\widehat{ABM}=\widehat{HBM}\)
Do đó: ΔABM=ΔHBM
b: Ta có: ΔABM=ΔHBM
nên AM=HM
mà HM<CM
nên AM<CM
c:
Ta có: ΔBAM=ΔBHM
nên BA=BH
Xét ΔAME vuông tại A và ΔHMC vuông tại H có
MA=MH
\(\widehat{AME}=\widehat{HMC}\)
Do đó: ΔAME=ΔHMC
Suy ra: ME=MC và AE=HC
Ta có: BA+AE=BE
BH+HC=BC
mà BA=BH
và AE=HC
nên BE=BC
Ta có: BE=BC
nên B nằm trên đường trung trực của EC\(\left(1\right)\)
Ta có: ME=MC
nên M nằm trên đường trung trực của EC\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BM là đường trung trực của EC
hay BM\(\perp\)EC
Đúng 1
Bình luận (1)
a) Xét △ ABM và △ HBM có:
\(\widehat{BAM}=\widehat{BHM}=90^0\)
BM chung
\(\widehat{ABM}=\widehat{HBM}\) ( BM phân giác của \(\widehat{B}\) )
⇒ △ ABM = △ HBM ( ch - gn )
b) Vì △ ABM = △ HBM ( cmt )
⇒ AM = HM ( 2 cạnh tương ứng )
△ AME = ▲ CMH ( g - c - g )
⇒ AM = CM ( 2 cạnh tương ứng )
c) Gọi N là giao điểm của BM và CE
Cm △ EBN = △ CBN ( c - g - c ) ( tự chứng minh nha, mik mệt quá )
⇒ \(\widehat{ENB}=\widehat{CNB}\) ( 2 góc tương ứng )
mà \(\widehat{ENB}=\widehat{CNB}=180^0\) ( kề bù )
⇒ BN ⊥ CE
⇒ BM ⊥ CE ( M ∈ BN )
Đúng 0
Bình luận (1)
Cho Tam giác ABC có AB=AC, AM là tia phân giác của góc BAC
a)Chứng minh BM=MC
b)chứng minh AM vuông góc với BC
( Giup mình với nha)
a. Ta có: AB = AC
\(\Rightarrow\Delta ABC\) cân tại A.
Mà tia phân giác của góc cân đồng thời cắt cạnh đối tại trung điểm của nó.
Vậy: BM = MC.
b. Xét 2\(\Delta\): \(\Delta ABM\) và \(\Delta ACM\) có:
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{BAM}=\widehat{CAM}\left(gt\right)\\AM.chung\end{matrix}\right.\)
\(\Rightarrow\) \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Vậy \(\widehat{AMB}=\widehat{AMC}\)
Mà: \(\widehat{BMC}=180^o\)
Vậy: \(\widehat{AMB}=90^o\) hay \(AM\perp BC\)
Đúng 1
Bình luận (0)
a) Xét tam giác ABM và tam giác ACM, ta có:
AB = AC (gt)
AM: cạnh chung
Góc BAM = góc CAM (do AM là tia phân giác của góc BAC)
=> tam giác ABM = tam giác ACM (c.g.c)
=> BM = MC (2 cạnh tương ứng) (đpcm)
b) Xét tam giác ABC, ta có:
AB = AC (gt)
=> tam giác ABC cân tại A
Mà AM là tia phân giác góc BAC
=> AM cũng là đường cao ứng với BC
=> AM vuông góc BC (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = AC. AM là phân giác của góc A
a)Chứng minh BM = MC
b) Chứng minh AM vuông góc với BC
c) Kẻ MH vuông góc với AB, MK vuông góc với AC. Chứng minh MH = MK
d) Chứng minh tam giác BHM = tam giác CKM
Mik đang cần rất rất gấp, mong mọi người giúp đỡ mik
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay BM=CM
b: Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
MH=MK
Do đó: ΔBHM=ΔCKM
Đúng 3
Bình luận (1)
Tham khảo:
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay BM=CM
b: Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
ˆHAM=ˆKAMHAM^=KAM^
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
MH=MK
Do đó: ΔBHM=ΔCKM
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, có BM là đường phân giác. Vẽ MH vuông góc BC, MH cắt AB tại E. chứng minh : ABH = HBM. So sánh AM và CM. BM vuông góc EC. AH // EC.
cho tam giác ABC có góc b= góc c trên tia đối của tia BC lấy điểm M trên tia đối của tía CB lấy điểm N sao cho BM=CN. kẻ BE vuông góc với AM (E thuộc AM) kẻ BF vuông góc với AN (F thuộc AN). CHỨNG MINH RẰNG tam giác BME = tam giác CNE
Xét ΔABM và ΔACN co
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
=>góc M=góc N
Xét ΔBME vuông tại E và ΔCNF vuông tại F có
BM=CN
góc M=góc N
Do đó: ΔBME=ΔCNF
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, 2 đường cao BM, CN:
a, CMR: AN. AB= AM. AC
b, Lấy K trên BM sao cho AK vuông góc với BM. Lấy I trên CN sao cho AK vuông góc với BI. CMR: Tam giác AKI cân.
a: Xét ΔANC vuông tại N và ΔAMB vuông tại M có
góc NAC chung
=>ΔANC đồng dạng với ΔAMB
=>AN/AM=AC/AB
=>AN*AB=AM*AC
b: AK vuông góc BM thì K trùng với M rồi bạn
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, 2 đường cao BM, CN:
a, CMR: AN. AB= AM. AC
b, Lấy K trên BM sao cho AK vuông góc với BM. Lấy I trên CN sao cho AK vuông góc với BI. CMR: Tam giác AKI cân.























