Tìm tất cả các cặp số thực (x; y) thỏa mãn:
\(16x^2y^2=\left(y^4+1\right)\left(1+16x^4\right)\)
tìm tất cả các cặp số thực (x;y) sao cho y là số nhỏ nhất thoả mãn điều kiện \(x^2+5y^2+2y+4xy-3=0\)
\(x^2+5y^2+2y+4xy-3=0\)
\(\Leftrightarrow\)\((x^2+4xy+4y^2)+(y^2+2y+1)=4\)
\(\Leftrightarrow\)\((x+2y)^2+(y+1)^2=4\)
\(\Leftrightarrow\)\((x+2y)^2=4-(y+1)^2\)
\(\Leftrightarrow\)\((x+2y)^2=(2-y-1)(2+y+1)\)
\(\Leftrightarrow\)\((x+2y)^2=(1-y)(3+y)\)
\(Vì \) \((x+2y)^2\geq0\)
\(\Rightarrow\)\((1-y)(3+y)\geq0\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
1-y\geq0\\
3+y\geq0
\end{cases}\\
\begin{cases}
1-y\leq0\\
3+y\leq0
\end{cases}
\end{array} \right.\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
y\leq1\\
y\geq-3
\end{cases}\\
\begin{cases}
y\geq1\text{(Vô lí)}\\
y\leq-3\text{(Vô lí)}
\end{cases}
\end{array} \right.\)\(\Rightarrow\)\(-3\leq y\leq1\)
\(\text{Mà y là số nhỏ nhất}\)
\(\Rightarrow\)\(y=-3\)
\(\Rightarrow\)\(x+2.(-3)=0\text{ (Vì }(x+2y)^2\geq0)\)
\(\Rightarrow\)\(x=6\)
\(\text{Vậy cặp số (x,y) thỏa mãn yêu cầu bài toán là: (6;-3)}\)
Nếu mình đúng cho mình xin 1 like nha
Tìm tất cả các giá trị của tham số thực m để hệ phương trình ( x + 1 ) ( 3 x 2 + 5 x y ) = m x 2 + 4 x + 5 y = 3 có ít nhất một cặp nghiệm thực
A . - 13 16 ; 9 4
B . ( - ∞ ; 9 4 ]
C . - ∞ ; 9 4
D . - 1 ; 9 4
a) Tìm tất cả các số thực x sao cho x2 = 4.
b) Tìm tất cả các số thực x sao cho x3 = - 8.
a) \({x^2} = 4 = {2^2} = {\left( { - 2} \right)^2} \Leftrightarrow x = \pm 2\)
b) \({x^3} = - 8 = {\left( { - 2} \right)^3} \Leftrightarrow x = - 2.\)
- Chú ý:
Trong toán học, căn bậc chẵn của một số là một số lớn hơn 0. Do đó số âm không có căn bậc chẵn.
1)Tim tất cả các cặp số nguyên x,y thỏa mãn :(x+5)y-x=10
2)Tìm tất cả các cặp số nguyên c,d để tích của chúng bằng 5 lần tổng của chúng
tớ chỉ làm phần 1 thôi
1. ta có (x+5)y-x=10
=>(x+5)y-x-5=10-5
=>(x+5)y-(x+5)=5
=>(x+5)(y-1)=5
lập bảng xét giá trị của x,y \(\in Z\)
Bạn tự làm tiếp nhé -_-
Tìm tất cả các cặp số thực (x, y) thỏa mãn x+y=3 và x3+y3= 9
ta có x3+y3=(x+y)(x2-xy+1)=9
mà x+y=3 => x2-xy+1=3 => x2-xy=2 => x(x-y)=2
x,y là số thực => x-y là số thực => x;x-y \(\inƯ_{\left(2\right)}=\left\{-2;-1;1;2\right\}\)
với x=-2 => không có giá trị y thỏa mãn
với x=-1 => không có giá trị y thỏa mãn
với x=1; x+y=3 => y=2
với x=2; x+y=3 => y=1
vậy (x;y)=(1;2);(2;1)
x + y = 3 => y = 3 - x
x3 + y3 = 9
<=> x3 + ( 3 - x )3 = 9
<=> x3 - x3 + 9x2 - 27x + 27 - 9 = 0
<=> 9x2 - 27x + 18 = 0
<=> 9( x2 - 3x + 2 ) = 0
<=> 9( x2 - x - 2x + 2 ) = 0
<=> 9[ x( x - 1 ) - 2( x - 1 ) ] = 0
<=> 9( x - 2 )( x - 1 ) = 0
<=> \(\orbr{\begin{cases}x-2=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}\)
Với x = 2 => 2 + y = 3 => y = 1
Với x = 1 => 1 + y = 3 => y = 2
Vậy các cặp số ( x ; y ) thỏa mãn là : ( 2 ; 1 ) , ( 1 ; 2 )
Ta có : \(x+y=3\) \(\Rightarrow\) \(x=3-y\)
\(x^3+y^3=9\)
\(\Leftrightarrow\) \(\left(x+y\right)\left(x^2-xy+y^2\right)=9\)
\(\Leftrightarrow\) \(3\left[\left(3-y\right)^2-\left(3-y\right)y+y^2\right]=9\)
\(\Leftrightarrow\) \(9-6y+y^2-3y+y^2+y^2=3\)
\(\Leftrightarrow\) \(3y^2-9y+6=0\)
\(\Leftrightarrow\) \(3\left(y-1\right)\left(y-2\right)=0\)
\(\Leftrightarrow\) \(\orbr{\begin{cases}y-1=0\\y-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}y=1;x=2\\y=2;x=1\end{cases}}}\)
Vậy hệ phương trình có ngiệm \(\left(x,y\right)=\left\{\left(2;1\right),\left(1;2\right)\right\}\)
Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 6 + m 2 ≥ 1 và x 2 + y 2 + 2 x - 4 y + 1 = 0 .
A. S = - 5 ; 5
B. S = - 7 ; - 5 ; - 1 ; 5 ; 7
C. S = - 5 ; - 1 ; 1 ; 5
D. S = - 1 ; 1
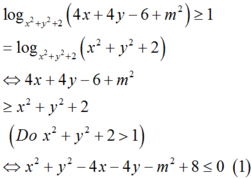
Ta có
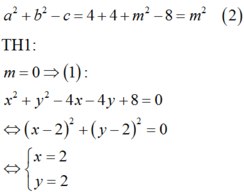
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
![]()
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
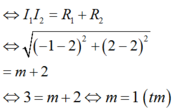
TH2: C1; C2 tiếp xúc trong và
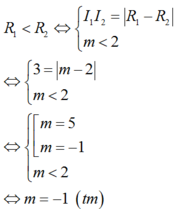
Vậy S = - 1 ; 1 .
Chọn D.
a)Tìm tất cả các cặp số nguyên x, y thỏa mãn:x(2y+3)=y+1
b) Tìm tất cả các số nguyên của x thỏa mãn:(-1)+3(-5)+7 ...+ x = 2002
a) => 2xy +3x=y+1
=> 2xy+3x-y=1
=> x(2y+3) - 1/2 (2y+3) +3/2 =1
=> (x-1/2)(2y+3)=1-3/2= -1/2
=> (2x-1)(2y+3)=-1
ta có bảng
...........
Tìm tất cả các cặp số nguyên x, y thỏa mãn: x3 + x = y
Tìm tất cả các cặp số nguyên x,y sao cho : x-2xy + y = 0
\(\Rightarrow2x-4xy+2y=0\\ \Rightarrow2x\left(1-2y\right)+2y-1=-1\\ \Rightarrow2x\left(1-2y\right)-\left(1-2y\right)=-1\\ \Rightarrow\left(2x-1\right)\left(2y-1\right)=1=1.1=\left(-1\right)\left(-1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=1\\2y-1=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\rightarrow\left(1;1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=-1\\2y-1=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\rightarrow\left(0;0\right)\)
Vậy các cặp \(\left(x;y\right)\) cần tìm là \(\left(1;1\right);\left(0;0\right)\)
tìm tất cả các cặp số nguyên x, y thỏa mãn x2+x = 32019y+1
- Với \(y=0\Rightarrow x^2+x=3^0+1=2\)
\(\Rightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
- Với \(y< 0\Rightarrow3^{2019y}\) không phải số nguyên \(\Rightarrow3^{2019y}+1\) không phải số nguyên (loại)
- Với \(y>0\Rightarrow3^{2019y}⋮3\Rightarrow3^{2019y}+1\) chia 3 dư 1
Mà \(x^2+x=x\left(x+1\right)\) là tích 2 số nguyên liên tiếp nên chia 3 chỉ có thể dư 0 hoặc 2
\(\Rightarrow x^2+x\ne3^{2019y}+1\) với mọi \(y>0\) \(\Rightarrow\) phương trình ko có nghiệm nguyên
Vậy pt đã cho có đúng 2 cặp nghiệm nguyên là \(\left(x;y\right)=\left(-2;0\right);\left(1;0\right)\)
@ Ha Dung vì khi y < 0 thì y = -k (k N)
⇒ 32019y = 3-2019k = ( N)
()2019k không phải là số nguyên vậy 32019y không phải là số nguyên em nhé.