a: Thay k=-3 vào pt, ta được:

\(x^2-2\cdot\left(-3+2\right)x+\left(-3\right)^2+2\cdot\left(-3\right)-7=0\)

\(\Leftrightarrow x^2+2x-4=0\)

\(\Leftrightarrow\left(x+1\right)^2=5\)

hay \(x\in\left\{\sqrt{5}-1;-\sqrt{5}-1\right\}\)

b: \(\text{Δ}=\left(2k+4\right)^2-4\left(k^2+2k-7\right)\)

\(=4k^2+16k+16-4k^2-8k+28\)

=8k+44

Để phương trình có hai nghiệm thì 8k+44>=0

=>8k>=-44

hay k>=-11/2

Theo đề, ta có: \(\left(x_1+x_2\right)^2-3x_1x_2=28\)

\(\Leftrightarrow\left(2k+4\right)^2-3\cdot\left(k^2+2k-7\right)=28\)

\(\Leftrightarrow4k^2+16k+16-3k^2-6k+21=28\)

\(\Leftrightarrow k^2+10k+37-28=0\)

\(\Leftrightarrow\left(k+1\right)\left(k+9\right)=0\)

=>k=-1

\(\text{Δ}=\left(2k+1\right)^2-4\left(k^2+4\right)\)

\(=4k^2+4k+1-4k^2-16=4k-15\)

Để phương trình có hai nghiệm phân biệt thì 4k-15>0

=>k>15/4

\(x_1^2+x_2^2=63\)

=>(x1+x2)^2-2x1x2=63

=>(2k+1)^2-2(k^2+4)=63

=>4k^2+4k+1-2k^2-8=63

=>2k^2+4k-7-63=0

=>2k^2+4k-70=0

=>k^2+2k-35=0

=>(k+7)(k-5)=0

=>k=-7(loại) hoặc k=5(nhận)

PT có 2 nghiệm \(\Leftrightarrow\Delta'=\left(k-2\right)^2-\left(-2k-5\right)\ge0\)

\(\Leftrightarrow k^2-4k+4+2k+10\ge0\\ \Leftrightarrow k^2-2k+14\ge0\\ \Leftrightarrow k\in R\)

Vậy PT luôn có 2 nghiệm

Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(k-2\right)\left(1\right)\\x_1x_2=-2k-5\left(2\right)\end{matrix}\right.\)

Lại có \(2x_1-x_2=7\left(3\right)\)

\(\left(1\right)\left(3\right)\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\left(k-2\right)\\2x_1-x_2=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1=2k+3\\x_2=2x_1-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2k+3}{2}\\x_2=\dfrac{4k+6}{2}-7=\dfrac{4k-8}{2}=2k-4\end{matrix}\right.\)

Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2k+3\right)\left(2k-4\right)}{2}=-2k-5\)

\(\Leftrightarrow\left(2k+3\right)\left(k-2\right)=-2k-5\\ \Leftrightarrow2k^2-k-6+2k+5=0\\ \Leftrightarrow2k^2+k-1=0\\ \Leftrightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-1\end{matrix}\right.\)

a) xét delta phẩy ta có:

1 + m - 2 = m -1 để phương trình có 2 nghiệm phân biệt thì delta phẩy >0 

=> m-1>0 => m > 1 

b) theo Vi-ét ta có:

\(\left\{{}\begin{matrix}x1+x2=2\\x1x2=2-m\end{matrix}\right.\)

theo bài ra ta có: x1² - x2² = 8 

<=> (x1-x2).(x1+x2)= 8 

<=>  2(x1-x2) = 8 <=> x1-x2 = 4 

<=> (x1-x2)² = 16 <=> x1² + x2² - 2x1x2 = 16

<=> (x1+x2)² - 4x1x2 = 16 <=> 4 - 4.(2m - 1 ) = 16 

<=> 4 - 8m + 4 = 16 <=> 8m = -8 

=> m = -1 

vậy m = -1 thỏa mãn x1² - x2² = 8 

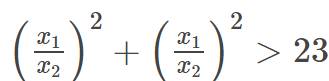
Lời giải:

Để pt có 2 nghiệm $x_1,x_2$ thì: $\Delta=k^2-8\geq 0$

$\Leftrightarrow k^2\geq 8(1)$

Áp dụng định lý Viet: 

$x_1+x_2=-k$

$x_1x_2=2$
Khi đó:
$(\frac{x_1}{x_2})^2+(\frac{x_2}{x_1})^2> 23$

$\Leftrightarrow \frac{x_1^4+x_2^4}{(x_1x_2)^2}>23$
$\Leftrightarrow x_1^4+x_2^4> 23(x_1x_2)^2=23.2^2=92$

$\Leftrightarrow (x_1^2+x_2^2)^2-2(x_1x_2)^2> 92$
$\Leftrightarrow (x_1^2+x_2^2)^2-8> 92$

$\Leftrightarrow [(x_1+x_2)^2-2x_1x_2]^2>100$

$\Leftrightarrow (k^2-4)^2>100$

$\Leftrightarrow k^2-4>10$ hoặc $k^2-4<-10$

$\Leftrightarrow k^2>14$ hoặc $k^2<-6$ (loại) 

$\Leftrightarrow k> \sqrt{14}$ hoặc $k< -\sqrt{14}$

Kết hợp với $k^2\geq 8$ suy ra $k> \sqrt{14}$ hoặc $k< -\sqrt{14}$

\(x^2-\left(m+3\right)x-m+5=0\)

Theo Vi-ét, ta có :

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m+3\\x_1x_2=\dfrac{c}{a}=-m+5\end{matrix}\right.\)

Ta có :

\(x_1^2x_2+x_1x_2^2=7\)

\(\Leftrightarrow x_1x_2\left(x_1+x_2\right)-7=0\)

\(\Leftrightarrow\left(-m+5\right)\left(m+3\right)-7=0\)

\(\Leftrightarrow-m^2-3m+5m+15-7=0\)

\(\Leftrightarrow-m^2+2m+8=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)