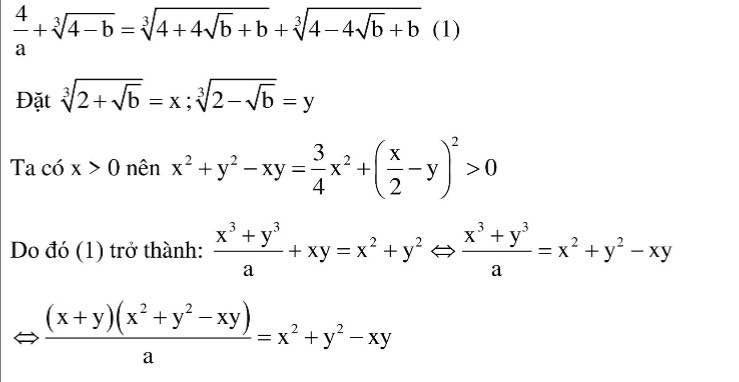Tìm nghiệm nguyên dương: \(\sqrt{x+3\sqrt{3}}=\sqrt{y}+\sqrt{z}\)

Những câu hỏi liên quan
Tìm nghiệm nguyên dương của phương trình : \(\sqrt{x+2\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
\(\Rightarrow x+2\sqrt{3}=y+z+2\sqrt{yz}\)
\(\Rightarrow2\sqrt{yz}=\left(x-y-z\right)+2\sqrt{3}\)
\(\Rightarrow4yz=\left(x-y-z\right)^2+12+4\sqrt{3}\left(x-y-z\right)\)
\(\Rightarrow4\sqrt{3}\left(x-y-z\right)=4yz-12-\left(x-y-z\right)^2\) (1)
\(\sqrt{3}\) là số vô tỉ nên đẳng thức xảy ra khi: \(x-y-z=0\)
Thay ngược vào (1) \(\Rightarrow yz=3\Rightarrow\left(y;z\right)=\left(1;3\right);\left(3;1\right)\)
\(\Rightarrow\sqrt{x+2\sqrt{3}}=\sqrt{4+2\sqrt{3}}\Rightarrow x=4\)
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương của phương trình \(\sqrt{x+2\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
Tìm nghiệm nguyên dương của phương trình \(\sqrt{x+y+3}+1=\sqrt{x}+\sqrt{y}\).
\(\sqrt{x+y+3}+1=\sqrt{x}+\sqrt{y}\)
Bình phương 2 vế, ta có:
\(x+y+3+1=x+y\)
\(x+y+3+1-x-y=0\)
\(4=0\) (vô lý)
Vậy phương trình vô nghiệm
-Chúc bạn học tốt-
Đúng 0
Bình luận (3)
(x,y) hoán vị của (4,9) . có vẻ hoạt động
Đúng 0
Bình luận (0)
Cho các số nguyên dương x,y,z thỏa mãn x+y+z<=3
Tìm giá trị lớn nhất \(A=\sqrt{1+x^2}+\sqrt{1+y^2}+\sqrt{1+z^2}+3\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)\)
Cho ba số nguyên dương x,y,z thỏa mãn:\(\frac{1}{\sqrt{2x-3}}+\frac{4}{\sqrt{y-z}}+\frac{16}{\sqrt{3z-1}}+\sqrt{2x-3}+\sqrt{y-2}+\sqrt{3z-1}=14\)
Tìm x,y,z
Đặt \(a=\sqrt{2x-3}\) ; \(b=\sqrt{y-2}\) ; \(c=\sqrt{3z-1}\) (\(a,b,c>0\))
Ta có : \(\frac{1}{a}+\frac{4}{b}+\frac{16}{c}+a+b+c=14\)
\(\Leftrightarrow\left(\sqrt{2x-3}+\frac{1}{\sqrt{2x-3}}-2\right)+\left(\sqrt{y-2}+\frac{4}{\sqrt{y-2}}-4\right)+\left(\sqrt{3z-1}+\frac{16}{\sqrt{3z-1}}-8\right)=0\)
\(\Leftrightarrow\left[\frac{\left(2x-3\right)-2\sqrt{2x-3}+1}{\sqrt{2x-3}}\right]+\left[\frac{\left(y-2\right)-4\sqrt{y-2}+4}{\sqrt{y-2}}\right]+\left[\frac{\left(3z-1\right)-8\sqrt{3z-1}+16}{\sqrt{3z-1}}\right]=0\)
\(\Leftrightarrow\frac{\left(\sqrt{2x-3}-1\right)^2}{\sqrt{2x-3}}+\frac{\left(\sqrt{y-2}-2\right)^2}{\sqrt{y-2}}+\frac{\left(\sqrt{3z-1}-4\right)^2}{\sqrt{3z-1}}=0\)
\(\Leftrightarrow\hept{\begin{cases}\left(\sqrt{2x-3}-1\right)^2=0\\\left(\sqrt{y-2}-2\right)^2=0\\\left(\sqrt{3z-1}-4\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\\z=\frac{17}{3}\end{cases}}}\)(TMĐK)
Vậy : \(\left(x;y;z\right)=\left(2;6;\frac{17}{3}\right)\)
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương của phương trình:
\(\sqrt{x+2\sqrt{3}=\sqrt{x}+\sqrt{y}}\)
tìm x y nguyên dương sao cho \(\sqrt{x}+\sqrt{y-z}+\sqrt{z-x}=\frac{1}{2}\left(y+3\right)\)
Dùng thẳng cô si vào VT luôn cho nhanh :v!
ĐK: \(x,y,z>0\)
Ta có: \(VP=\frac{1}{2}\left(y+3\right)=\frac{y+3}{2}\)
Mặt khác theo cô si,ta có
\(VT\le\frac{1+x}{2}+\frac{1+y-z}{2}+\frac{1+z-x}{2}\)\(=\frac{y+3}{2}=VP\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x=1\\y-z=1\\z-x=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y-z=1\\z-1=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\z=2\\y-2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=3\\z=2\end{cases}}\)
Vậy ...
Quá nhanh quá ngu hiểm :v.Lâu lắm mới nghĩ ra được cách thế này.Nãy ngồi bình phương suốt mà làm hoài không ra.
Đúng 0
Bình luận (0)
1. Tìm các số nguyên dương a; b sao cho:dfrac{4}{a} + 3sqrt{4-b} 3sqrt{4+4sqrt{b}+b} + 3sqrt{4-4sqrt{b}+b}2. Giải phương trình nghiệm nguyênx^3-y^3-6x^2+12x27
Đọc tiếp
1. Tìm các số nguyên dương a; b sao cho:
\(\dfrac{4}{a}\) \(+\) 3\(\sqrt{4-b}\) \(=\) 3\(\sqrt{4+4\sqrt{b}+b}\) \(+\) 3\(\sqrt{4-4\sqrt{b}+b}\)
2. Giải phương trình nghiệm nguyên
\(x^3-y^3-6x^2+12x=27\)
đăng câu hỏi kiểu j mà đặng đc lên như thế này đấy
Đúng 0
Bình luận (0)
1.
Đặt \(\sqrt[3]{2+\sqrt{b}}=x;\sqrt[3]{2-\sqrt{b}}=y\)
Do \(x>0\Rightarrow x^2+y^2-xy=\dfrac{3}{4}x^2+\left(\dfrac{1}{2}x-y\right)^2>0\)
\(PT\Leftrightarrow\dfrac{x^3+y^3}{a}+xy=x^2+y^2\Leftrightarrow\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{a}=x^2-xy+y^2\\ \Leftrightarrow\left(x^2-xy+y^2\right)\left(\dfrac{x+y}{a}-1\right)=0\\ \Leftrightarrow\dfrac{x+y}{a}=1\\ \Leftrightarrow\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}=a\left(1\right)\\ \Leftrightarrow\left(\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}\right)^3=a^3\\ \Leftrightarrow4+3a\sqrt[3]{4-b}=a^3\left(2\right)\\ \Rightarrow4-b=\left(\dfrac{a^3-4}{3a}\right)^3\)
Mặt khác \(b\in \mathbb{Z^+}\)
\(\Rightarrow\left(a^3-4\right)⋮3a\Rightarrow\left(a^3-4\right)⋮a\\ \Rightarrow4⋮a\Rightarrow a\in\left\{1;2;4\right\}\)
Với \(a=1\Rightarrow4-b=1\Rightarrow b=5\)
Với \(a=2;a=4\Rightarrow b\notin \mathbb{Z}\)
Vậy \(\left(a;b\right)=\left(1;5\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
TÌm nghiệm nguyên dương của hệ phương trình
\(\hept{\begin{cases}z+y=x+10\\yz=10x+1\end{cases}}\)
\(\hept{\begin{cases}x+y+z=100\\5x+3y+\frac{z}{3}=100\end{cases}}\)
Tính
\(\sqrt{2x+1}+3\sqrt{4x^2-2x+1}=3+\sqrt{8x^2+1}\)
\(\sqrt{x^2+3}-\sqrt{6-x^2}=3+\sqrt{\left(x^2+3\right).\left(6-x^2\right)}\)