Cho \(\Delta ABC=\Delta DÈF\). Tính chu vi mỗi \(\Delta\), biết ràng AB = 5cm, BC = 7cm, DF = 6 cm

Những câu hỏi liên quan
Cho ΔABC ∼ ΔDEF. Biết AB = 3cm, BC = 5cm, AC = 7cm; DF = 9,5cm. Tính các cạnh của Δ DEF và tính tỉ số chu vi của 2 Δ trên
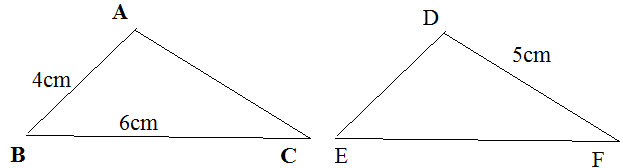
Cho \(\Delta ABC=\Delta DEF\). Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó) ?
Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)
Đúng 0
Bình luận (0)
Ta có \(\Delta\)ABC= \(\Delta\)DEF
Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.
Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)
Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm )
Đúng 0
Bình luận (0)
vì tam giác ABC = tam giác DEF
Nên AB = DE= 4cm
BC= EF = 6 cm
AC= DF = 5 cm
lúc đó:chu vi tam giác ABC= tam giác DEF= 4+5+6=15(cm)
Vậy chu vi tam giác ABC = chu vi tam giác DEF=15cm
Đúng 0
Bình luận (0)
Cho ΔABC = ΔDEF. Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi mỗi tam giác là tổng độ dài ba cạnh của tam giác đó).
Hình vẽ
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Vậy...
Chúc bạn học tốt!
AC1/Cho ΔABC ΔDEF. Tính chu vi mỗi Δ biết AB4 cm, BC6cm, DF5cm
2/ Cho ΔABC có ABAC. Trên ÁC lấy điểm D sao cho ADAB. Gọi M là trug điểm BD
a/ C/m ΔABMΔADM
b/ C/m AM⊥BD
c/ Tia AM cắt BC tại K. C/m ΔABKΔADK
d/ Trên tia đối của tia BA lấy điểm F sao cho BFDC. C/m 3 điểm F,K,C thẳng hàng.
3/ Cho ΔABC vuông tại A, góc B60 độ. Trên tia BA lấy điểm E sao cho BEBC. Vẽ BI là phân giác góc B, I thuộc AC
a/. C/m tam giác BEC đều
b/ IE IC
c/ EI⊥BC
Đọc tiếp
AC1/Cho ΔABC = ΔDEF. Tính chu vi mỗi Δ biết AB=4 cm, BC=6cm, DF=5cm
2/ Cho ΔABC có AB<AC. Trên ÁC lấy điểm D sao cho AD=AB. Gọi M là trug điểm BD
a/ C/m ΔABM=ΔADM
b/ C/m AM⊥BD
c/ Tia AM cắt BC tại K. C/m ΔABK=ΔADK
d/ Trên tia đối của tia BA lấy điểm F sao cho BF=DC. C/m 3 điểm F,K,C thẳng hàng.
3/ Cho ΔABC vuông tại A, góc B=60 độ. Trên tia BA lấy điểm E sao cho BE=BC. Vẽ BI là phân giác góc B, I thuộc AC
a/. C/m tam giác BEC đều
b/ IE= IC
c/ EI⊥BC
Bài 2 :
a) Xét \(\Delta ABM,\Delta ADM\) có :
\(AB=AD\left(gt\right)\)
\(AM:chung\)
\(BM=DM\) (M là trung điểm của BD)
=> \(\Delta ABM=\Delta ADM\left(c.c.c\right)\)
b) Từ \(\Delta ABM=\Delta ADM\) (cmt - câu a) suy ra :
\(\widehat{AMB}=\widehat{AMD}\) (2 góc tương ứng)
Mà : \(\widehat{AMB}+\widehat{AMD}=180^o\left(Kềbù\right)\)
=> \(\widehat{AMB}=\widehat{AMD}=\dfrac{180^o}{2}=90^o\)
=> \(AM\perp BD\rightarrowđpcm\)
c) Xét \(\Delta ABK,\Delta ADK\) có :
AB = AD (gt)
\(\widehat{BAK}=\widehat{DAK}\) (\(\Delta ABM=\Delta ADM\))
AK :Chung
=> \(\Delta ABK=\Delta ADK\left(c.g.c\right)\)
d) Ta có : \(\left\{{}\begin{matrix}\widehat{ABK}+\widehat{FBK}=180^{^O}\\\widehat{ADK}+\widehat{CDK}=180^{^O}\end{matrix}\right.\left(Kềbù\right)\)
Lại có : \(\widehat{ABK}=\widehat{ADK}\) (do \(\Delta ABK=\Delta ADK\left(c.g.c\right)\)
Nên : \(180^o-\widehat{ABK}=180^o-\widehat{ADK}\)
\(\Leftrightarrow\widehat{FBK}=\widehat{CDK}\)
Xét \(\Delta BFK,\Delta DCK\) có :
\(BF=CD\left(gt\right)\)
\(\widehat{FBK}=\widehat{CDK}\left(cmt\right)\)
\(BK=DK\) (\(\Delta ABK=\Delta ADK\left(c.g.c\right)\))
=> \(\Delta BFK=\Delta DCK\left(c.g.c\right)\)
=> FK = DK (2 cạnh tương ứng)
=> K là trung điểm của FD
=> F, D, K thẳng hàng.
Đúng 0
Bình luận (0)
Cho \(\Delta ABC=\Delta DEH\). Biết AB = 5cm, AC = 6cm, chu vi tam giác DEH bằng 19 cm. Tính độ dài các cạnh của tam giác DEH ?
Vì tam giác ABC = tam giác DEH
=> AB=De
Đúng 0
Bình luận (0)
Tam giác ABC = Tam giác DEH (gt)
=> AB = DE (2 cạnh tương ứng) mà AB = 5 (cm) => DE = 5 (cm)
AC = DH (2 cạnh tương ứng) mà AC = 6 (cm) => DH = 6 (cm)
SDEH = 19
DE + DH + EH = 19
5 + 9 + EH = 19
EH = 19 - 9 - 5
EH = 5 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC =tam giác DEF. Tính chu vi mỗi tam giác, biết rằng AB = 5cm, BC=7cm, DF = 6cm.
Xét ΔABC=ΔDEFcó:
AB=DE=5cm
BC=EF=7cm
DF=AC=6cm
- Chu vi của tam giác ABC là:
AB+BC+AC=5+7+6=18(cm)
- Chu vi của tam giác DEF là:
DE+EF+DE=5+7+6=18(cm)
Vậy +)Chu vi của tam giác ABC là 18 cm
+) Chu vi của tam giác DEF là 18 cm
Đúng 0
Bình luận (0)
Cho Δ ABC, D ∈ AB sao cho AD =\(\frac{2}{3}\)DB. Qua D kẻ đường thẳng song song với BC cắt AC ở E.
a) CMR: Δ ADE đồng dạng Δ ABC. Tìm tỷ số đồng dạng của 2 Δ trên
b) Tính chu vi Δ ADE, biết chu vi Δ ABC là 60 cm
Bài 2. Cho ABC =DEF, biết AB =7cm ,BC =5cm ,DF =6cm
. a) Tính các cạnh còn lại của mỗi tam giác.
b) Tính chu vi của mỗi tam giác.
a) Các cạnh còn lại của mỗi tam giác:
-Tam giác ABC: cạnh AC=6cm
-Tam giác DEF:cạnh DE=7cm,cạnh EF=5cm
b)Chu vi của mỗi tam giác đều bằng:18cm
Đúng 1
Bình luận (0)
a)Δ A B C = Δ D E F c ó :
A B = D E = 5 c m
B C = E F = 7 c m
D F = A C = 6 c m
b)- Chu vi của tam giác A B C là:
A B + B C + A C = 5 + 7 + 6 = 18 ( c m )
- Chu vi của tam giác D E F là:
D E + E F + D E = 5 + 7 + 6 = 18 ( c m )
Đúng 0
Bình luận (1)
Vì ΔABC = ΔDEF (gt)
=> AC = DF = 6cm
Chu vi ΔABC là: AB + BC + AC = 5 + 7 + 6 = 18(cm)
Lại có: ΔABC = ΔDEF(gt)
=> chu vi ΔABC = chu vi ΔDEF = 18cm
Vậy chu vi ΔABC : 18cm
chu vi ΔDEF: 18cm
Đúng 1
Bình luận (0)
TAM GIÁC ĐỒNG DẠNG
1, a) Cho AB6 dm, AC15 cm , tìm tỉ số hai đoạn thẳng AB và AC .
b) Cho AB6 cm, AC18 cm , tìm tỉ số hai đoạn thẳng AB và AC .
2, ΔMNP _____ ΔABC thì : a) frac{MN}{AB}........ b) frac{MP}{AC}........
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm;...
Đọc tiếp
TAM GIÁC ĐỒNG DẠNG
1, a) Cho AB=6 dm, AC=15 cm , tìm tỉ số hai đoạn thẳng AB và AC .
b) Cho AB=6 cm, AC=18 cm , tìm tỉ số hai đoạn thẳng AB và AC .
2, ΔMNP _____ ΔABC thì : a) \(\frac{MN}{AB}=\)........ b) \(\frac{MP}{AC}=........\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
b) Cho \(\Delta ABC\) có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
5. a) Cho \(\Delta DEF\sim\Delta ABC\) theo tỉ số đồng dạng k = 2. Tìm tỉ số \(\frac{S_{DÈF}}{S_{ABC}}\)
b) Cho \(\Delta DEF\)\(\sim\Delta ABC\) theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số \(\frac{S_{DEF}}{S_{ABC}}\)
6. Cho \(\Delta ABC.\)Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho \(\frac{AD}{AB}=\frac{AE}{AC}.\)Kết luận nào sai ❓
A. \(\Delta ADE\sim\Delta ABC\) B. DE//BC C. \(\frac{AE}{AD}=\frac{AC}{AB}\) D. \(\Delta ADE=\Delta ABC\)
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.\(\Delta ABC\sim\Delta DEF\) B. \(\Delta ABC\sim\Delta EDF\)
C. \(\Delta ABC\sim\Delta DFE\) D.\(\Delta ABC\sim\Delta FED\)
giải giúp mình với! Mình cần gấp
TAM GIÁC ĐỒNG DẠNG
1, a) Tỉ số hai đoạn thẳng AB và AC : \(\frac{AB}{AC}=\frac{6}{15}\)
b) Tỉ số hai đoạn thẳng AB và AC . : \(\frac{AB}{AC}=\frac{6}{18}=\frac{1}{3}\)
2, ΔMNP ~ ΔABC thì : \(\frac{MN}{AB}=\frac{NP}{BC}=\frac{MP}{AC}\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
Bạn ơi D ở đâu vậy ?
b) Cho ΔABCΔABC có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
Xét \(\Delta ABC\) có AD là phân giác
\(\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\Rightarrow BD=\frac{AB.CD}{AC}=3cm\)
5. a) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k = 2. Tìm tỉ số SDÈFvà SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=2^2=4\)
b) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số SDEF và SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
6. Cho ΔABC..Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho AD/AB=AE/AC Kết luận nào sai ❓
A. ΔADE∼ΔABC B. DE//BC
C. AE/AD=AC/AB D. ΔADE=ΔABC
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.ΔABC∼ΔDEF B. ΔABC∼ΔEDF
C. ΔABC∼ΔDFE D.ΔABC∼ΔFED
Đúng 0
Bình luận (1)