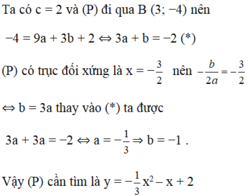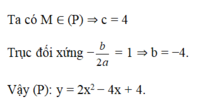Đề sai rồi bạn

Trục đối xứng là 2
=> -b/2a = 2
=> a = -b/4 = - (-4)/4 = 1
P đi qua A(1;2)
=> 2 = 1.1^2 - 4.1 + c
=> c + 1 - 4 = 2
=> c = 5
=> y = x^2 - 4x + 5

Đáp án A

\(\Leftrightarrow\left\{{}\begin{matrix}4a+c=2\\-\dfrac{b}{2a}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=2-4a=2-4\cdot\left(-1\right)=6\\a=-1\end{matrix}\right.\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}9a+3b=-6\\\dfrac{b}{2a}=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+b=-2\\3a=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{3}\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(P\right):y=-\dfrac{1}{3}x^2-x+2\\ b,\Leftrightarrow\left\{{}\begin{matrix}4a+2b=-3\\-\dfrac{b}{2a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+2b=-3\\4a-b=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{4}\\b=-1\end{matrix}\right.\Leftrightarrow\left(P\right):y=-\dfrac{1}{4}x^2-x+2\)

Lời giải:
$(P):y=x^2+bx+2$ đi qua $(3;-4)$ nên:

$-4=3^2+b.3+2\Rightarrow b=-5$

Vậy pt cần tìm là $y=x^2-5x+2$

Vậy thì trục đối xứng $x=\frac{-3}{2}$ có vẻ thừa?

\(\left(P\right):y=ax^2+bx+2\)

Vì (P) đi qua điểm \(M\left(1;5\right)\) nên ta có: \(a.1^2+b.1+2=5\Leftrightarrow a+b=3\)    (1)

Mà (P) có trục đối xứng là \(x=\dfrac{-1}{4}\) nên:   \(\dfrac{-b}{2a}=\dfrac{-1}{4}\)

\(\Leftrightarrow-2a=-4b\Leftrightarrow-2a+4b=0\)                 (2)

Từ (1) và (2) ta có:  

\(\left\{{}\begin{matrix}a+b=3\\-2a+4b=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)

Vậy parabol cần tìm có dạng:  \(y=2x^2=x+2\)

Đáp án A

+ Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2

⇒ –b/2a = –3/2 ⇒ b = 3a (1)

+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)

⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).

Thay b = 3a ở (1) vào biểu thức (2) ta được:

9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.

Vậy parabol cần tìm là y = –1/3x2 – x + 2.

Lời giải:
Parabol đi qua $A(2;19)$ nên $y_A=3x_A^2+bx_A+c$ hay $19=12+2b+c$

$\Rightarrow 2b+c=7(1)$

$x=\frac{-2}{3}$ là trục đối xứng 

$\Leftrightarrow \frac{-b}{2.3}=\frac{-2}{3}$

$\Rightarrow b=4(2)$

Từ $(1); (2)\Rightarrow c=-1$

Vậy parabol có pt $y=3x^2+4x-1$

Theo đề, ta có:

\(\left\{{}\begin{matrix}\dfrac{-b}{6}=\dfrac{-2}{3}\\12+2b+c=19\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\c=-1\end{matrix}\right.\)

Bài 2: 

a: Theo đề, ta có:

\(\left\{{}\begin{matrix}a+b+c=0\\c=5\\\dfrac{-b}{2a}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-5\\b=-6a\\c=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-5a=-5\\b=-6a\\c=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-6\\c=5\end{matrix}\right.\)

b: Theo đề, ta có:

\(\left\{{}\begin{matrix}4a+2b+c=3\\\dfrac{-b}{2a}=3\\-\dfrac{b^2+4ac}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+2b+c=3\\b=-6a\\\left(-6a\right)^2+4ac=-16a\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4a-12a+c=3\\b=-6a\\36a^2+16a+4ac=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=8a+3\\b=-6a\\36a^2+16a+4a\left(8a+3\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{7}{17}\\b=6\cdot\dfrac{7}{17}=\dfrac{42}{17}\\c=8\cdot\dfrac{-7}{17}+3=-\dfrac{5}{17}\end{matrix}\right.\)