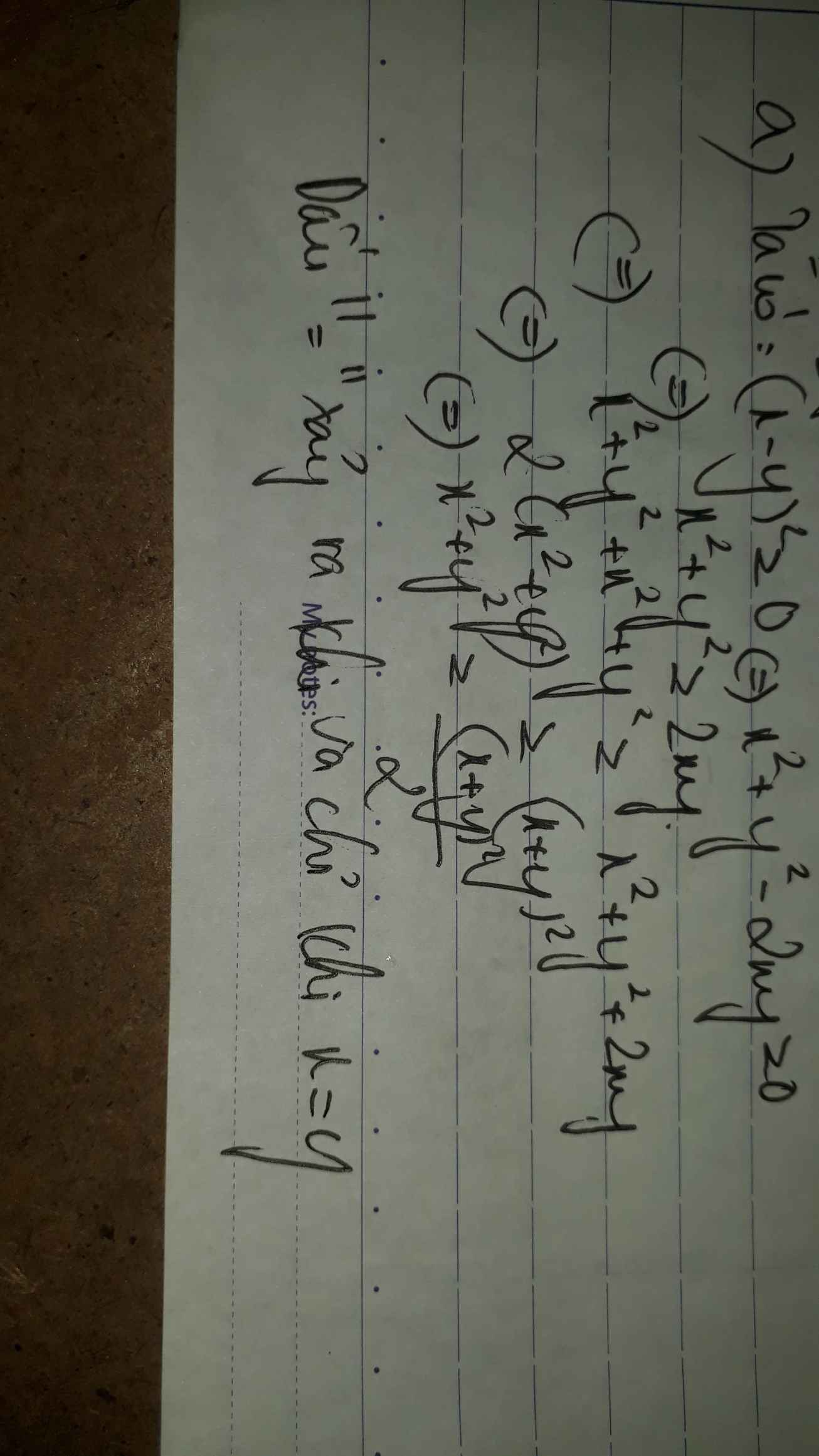\(BĐT\Leftrightarrow\left(\dfrac{x}{y+z}+1\right)+\left(\dfrac{y}{x+z}+1\right)+\left(\dfrac{z}{x+y}+1\right)\ge\dfrac{3}{2}+3=\dfrac{9}{2}\\ \Leftrightarrow\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)\ge9\left(1\right)\)

Áp dụng BĐT Cauchy:

\(\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\ge3\sqrt[3]{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)

\(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\ge3\sqrt[3]{\dfrac{1}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}\)

Nhân vế theo vế 2 BĐT ta được

\(\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)\ge3\cdot3\sqrt[3]{1}=9\)

Do đó \(\left(1\right)\) luôn đúng

Vậy ta được đpcm

Phải có thêm dữ kiện x,y,z > 0 nữa nhé.

Áp dụng BĐT C - S dạng Engel, ta có:

Cycma(x/(y + z)) = cycma(x^2/(xy + xz)) >= cycma(x)^2/(2cycma(xy)) >= cycma(x)^2/((2cycma(x)^2)/3) = 3/2 (đpcm)

đây là BĐT Nesbit cho 3 số thực dương nên thiếu điều kiện x,y,z\(\in R\)*

\(x^2+y^2+z^2+3\ge2\left(x+y+z\right)\)

\(\Leftrightarrow x^2+y^2+z^2+3\ge2x+2y+2z\)

\(\Leftrightarrow x^2+y^2+z^2+3-2x-2y-2z\ge0\)

\(\Leftrightarrow\left(x^2-2x+1\right)+\left(y^2-2y+1\right)+\left(z^2-2z+1\right)\ge0\)

\(\Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2\ge0\) (luôn đúng)

Vậy \(x^2+y^2+z^2+3\ge2\left(x+y+z\right)\)

cảm ơn bạn nhiều

Ta có : \(x^2+1\ge2x\) (1)

\(y^2+1\ge2y\) (2)

\(z^2+1\ge2z\) (3)

Cộng các vế của  (1) (2) (3) ta được :

\(x^2+y^2+z^2+3\ge2\left(x+y+z\right)\)

Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\)

\(\frac{x^2}{\sqrt{1-x^2}}=\frac{x^3}{\sqrt{x^2}.\sqrt{1-x^2}}\ge\frac{x^3}{\frac{x^2+1-x^2}{2}}=2x^3\)

Tương tự

\(\frac{y^2}{\sqrt{1-y^2}}\ge2y^3;\frac{z^2}{\sqrt{1-z^2}}\ge2z^3\)

Cộng vế theo vế

\(VT\ge2\left(x^3+y^3+z^3\right)=2\)

a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)

\(\Leftrightarrow2x^2+2y^2\ge\left(x+y\right)^2\Leftrightarrow x^2+y^2\ge2xy\)

\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\left(đúng\right)\)

b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)

\(\Leftrightarrow4x^3+4y^3\ge\left(x+y\right)^3\Leftrightarrow3x^3+3y^3\ge3x^2y+3xy^2\)

\(\Leftrightarrow3x^2\left(x-y\right)-3y^2\left(x-y\right)\ge0\)

\(\Leftrightarrow3\left(x-y\right)\left(x^2-y^2\right)\ge0\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\left(đúng\right)\)

a: Ta có: \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)

\(\Leftrightarrow2x^2+2y^2-x^2-2xy-y^2\ge0\)

\(\Leftrightarrow x^2-2xy+y^2\ge0\)

\(\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)

\(x^2+y^2>=2xy\Rightarrow\frac{x}{x^2+y^2}< =\frac{x}{2xy}=\frac{1}{2y}\)(1)

\(y^2+z^2>=2yz\Rightarrow\frac{y}{y^2+z^2}< =\frac{y}{2yz}=\frac{1}{2z}\)(2)

\(x^2+z^2>=2xz\Rightarrow\frac{z}{x^2+z^2}< =\frac{z}{2xz}=\frac{1}{2x}\)(3)

từ (1) (2) (3)\(\Rightarrow\frac{x}{x^2+y^2}+\frac{y}{y^2+z^2}+\frac{z}{x^2+z^2}< =\frac{1}{2y}+\frac{1}{2z}+\frac{1}{2x}=\frac{1}{2}\left(\frac{1}{y}+\frac{1}{z}+\frac{1}{x}\right)\)(đpcm)

bài này phải x;y;z dương

x²+y²z²>=2lxl.lyl.lzl nên VT>=6lxl.lyl.lzl>=6xyz

\(2\left(x^2+y^2+z^2+xy+yz+xz\right)=\left(x+y\right)^2+\left(y+z\right)^2+\left(z+x\right)^2\)

\(=\left(3-x\right)^2+\left(3-y\right)^2+\left(3-z\right)^2\)

\(=27-6\left(x+y+z\right)+x^2+y^2+z^2\)

\(=9+x^2+y^2+z^2\)

Dễ dàng CM được \(x^2+y^2+z^2\ge\frac{\left(x+y+z\right)^2}{3}=3\)

=>\(2\left(x^2+y^2+z^2+xy+yz+zx\right)\ge12\)

=> dpcm

Ta có: \(2\left(x^2+y^2+z^2+xy+yz+xz\right)\)

\(=2x^2+2y^2+2z^2+2xy+2yz+2xz\)

\(=\left(x^2+2xy+y^2\right)+\left(y^2+2yz+z^2\right)+\left(x^2+2xz+z^2\right)\)

\(=\left(x+y\right)^2+\left(y+z\right)^2+\left(x+z\right)^2\)(1)

Mà \(x+y+z=3\Rightarrow\hept{\begin{cases}x+y=3-z\\y+z=3-x\\x+z=3-y\end{cases}}\)

\(\Rightarrow\left(1\right)=\left(3-z\right)^2+\left(3-x\right)^2+\left(3-y\right)^2\)

\(=9-6z+z^2+9-6x+x^2+9-6y+y^2\)

\(=27-6\left(x+y+z\right)+x^2+y^2+z^2\)

\(=9+x^2+y^2+z^2\)

Áp dụng BĐT Cauchy cho 3 số:

\(x^2+y^2+z^2=\frac{x^2}{1}+\frac{y^2}{1}+\frac{z^2}{1}\ge\frac{\left(x+y+z\right)^2}{1+1+1}=\frac{3^2}{3}=3\)

\(\Rightarrow9+x^2+y^2+z^2\ge12\)

hay \(2\left(x^2+y^2+z^2+xy+yz+xz\right)\ge12\)

\(\Leftrightarrow x^2+y^2+z^2+xy+yz+xz\ge6\left(đpcm\right)\)

\(VT=3\left(x^2+y^2+z^2\right)-\left(x-y\right)^2-\left(y-z\right)^2-\left(z-x\right)^2=\left(x+y+z\right)^2\)

\(\Leftrightarrow3x^2+3y^2+3z^2-x^2+2xy-y^2-y^2+2yz-z^2-z^2+2xz-x^2=\left(x+y+z\right)^2\)

\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2xz=\left(x+y+z\right)^2\)* luôn đúng *

Vậ ta có đpcm