bài nào thế bạn?

Giải:

Chúc bạn học tốt!

Bài 19:

Chu vi hình vuông là: \(\left(12+6\right)\cdot2=36\left(cm\right)\)

Độ dài cạnh hình vuông là 36/4=9(cm)

Diện tích hình vuông là \(9^2=81\left(cm^2\right)\)

Bài 20:

Độ dài đường cao là \(\dfrac{160}{4}=40\left(m\right)\)

Diện tích miếng đất là: \(60\cdot40=2400\left(m^2\right)=0,24\left(ha\right)\)

Khối lượng ngô thu hoạch được là:

\(0,24:3\cdot13,5=1,08\left(tấn\right)=1080\left(kg\right)\)

3, enough warm
5, enough money
9,enough far

1. hard enough

2. well enough

3. warm enough

4. rich enough

5. enough money

6. enough time

7. strong enough

8. enough French

9. far enough

10. enough chairs

(P/s: nãy h ngồi làm mợt lắm á , tick cho tui nghen (～￣▽￣)～)

20. B   21. A   22. C.-.   23. B   24. D   25. B   26. C   27. B
*Writing
39. Took
40. => My son is keen on reading books than playing computer games.
41. => Tennis player Novak Djokovic is skillful.
42. I went to Da Nang last summer vacation.
43. All children shouldn't spend much time on these video games.
44. Martin got a bad toothache because he forgot to brush his teeth.
 

Bài 5: 

a: BC=10cm

b: HA=4,8cm

HB=3,6(cm)

HC=6,4(cm)

Bài 6:

\(x^3=6+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow x^3=6+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=6\\ y^3=34+3\sqrt[3]{\left(17+12\sqrt{2}\right)\left(17-12\sqrt{2}\right)}\left(\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}\right)\\ \Leftrightarrow y^3=34+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=34\\ \Leftrightarrow P=x^3-3x+y^3-3y+1980=6+34+1980=2020\)

gfrưerrrrrrrrrrr

\(\left\{{}\begin{matrix}2x+y=1\\x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x+y=-1\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)

\(\left\{{}\begin{matrix}2x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=9\\x-y=-6\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}2x=3\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{15}{2}\end{matrix}\right.\)\(\left\{{}\begin{matrix}2x+3y=6\\x-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+6y=12\\3x-6y=9\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}7x=21\\3x-6y=9\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)

a) ĐKXĐ: \(x>0;x\ne\pm1.\)

\(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{1-x}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\right).\\ A=\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\)

\(A=\dfrac{2x+1}{4\sqrt{x}}.\)

b) \(A=\dfrac{3}{4}.\Rightarrow\dfrac{2x+1}{4\sqrt{x}}=\dfrac{3}{4}.\Rightarrow12\sqrt{x}-8x+4=0.\\ \Leftrightarrow8x-12\sqrt{x}-4=0.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=\dfrac{3+\sqrt{17}}{4}.\\\sqrt{x}=\dfrac{3-\sqrt{17}}{4}.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{13+3\sqrt{17}}{8}.\\x=\dfrac{13-3\sqrt{17}}{8}.\end{matrix}\right.\) (TM). 

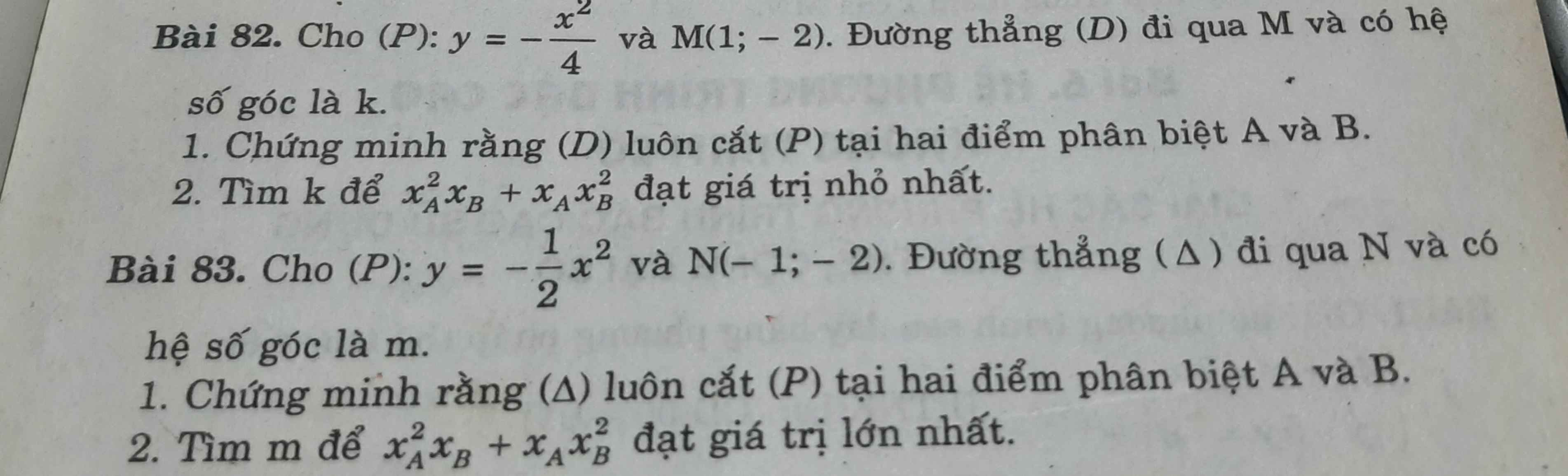
Phương trình (D) có dạng:

\(y=k\left(x-1\right)-2\Leftrightarrow y=kx-k-2\)

Phương trình hoành độ giao điểm (P) và (D):

\(-\dfrac{x^2}{4}=kx-k-2\Leftrightarrow x^2+4kx-4\left(k+2\right)=0\) (1)

\(\Delta'=4k^2+4\left(k+2\right)=\left(2k+1\right)^2+7>0\) ; \(\forall k\)

\(\Rightarrow\) (1) luôn có 2 nghiệm pb hay (D) luôn cắt (P) tại 2 điểm pb A và B

b. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-4k\\x_Ax_B=-4\left(k+2\right)\end{matrix}\right.\)

Đặt \(A=x_A^2x_B+x_Ax_B^2=x_Ax_B\left(x_A+x_B\right)\)

\(A=-4\left(k+2\right).\left(-4k\right)=16\left(k^2+2k\right)=16\left(k+1\right)^2-16\ge-16\)

\(\Rightarrow A_{min}=-16\) khi \(k+1=0\Leftrightarrow k=-1\)