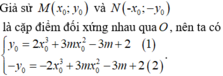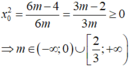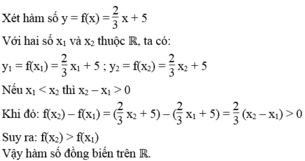Chứng minh rằng hàm số f(x) = 3x – sinx đồng biến trên ℝ.

Những câu hỏi liên quan
Chứng minh hàm số \(f\left(x\right)=x-sinx\) đồng biến trên \(\left[0;\dfrac{\pi}{2}\right]\)
Lời giải:
$f'(x)=1-\cos x\geq 0$ với mọi $x\in [0; \frac{\pi}{2}]$. Trong đó $f'(x)=1-\cos x=0$ chỉ xảy ra khi $x=0$ với điều kiện $x\in [0; \frac{\pi}{2}]$ nên hàm số $f(x)$ đồng biến trên $[0; \frac{\pi}{2}]$
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của để hàm số
y
x
+
m
(
sin
x
+
cos
x
)
đồng biến trên
ℝ
Đọc tiếp
Tìm tất cả các giá trị của để hàm số y = x + m ( sin x + cos x ) đồng biến trên ℝ
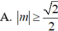
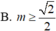
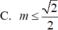
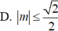
cho hàm số y=f(x)=3x-2, chứng minh hàm số luôn đồng biến trên R
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{3x_1-2-3x_2+2}{x_1-x_2}=3\)
Vậy: Hàm số đồng biến trên R
Đúng 1
Bình luận (0)
Hàm số \(y=f\left(x\right)=3x-2\) có \(a=3>0\) nên hàm số luôn đồng biến trên R.
Đúng 1
Bình luận (0)
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số y = f(x) = 2 3 x + 5 với x ∈ R. Chứng minh rằng hàm số đồng biến trên R.
Cho hàm số f(x) liên trục trên
ℝ
và có đồ thị như hình vẽ bên. Hàm số f(x) đồng biến trên khoảng nào ? A.
−
∞
;
0
.
B.
−
∞
;
−
1
.
C.
1
;...
Đọc tiếp
Cho hàm số f(x) liên trục trên ℝ và có đồ thị như hình vẽ bên. Hàm số f(x) đồng biến trên khoảng nào ?
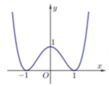
A. − ∞ ; 0 .
B. − ∞ ; − 1 .
C. 1 ; + ∞ .
D. − 1 ; 1 .
Đáp án C
Phương pháp giải: Dựa vào hình dáng của đồ thị để xét tính đơn điệu.
Lời giải: Dựa vào hình vẽ, ta thấy hàm số đồng biến trên khoảng - 1 ; 0 và 1 ; + ∞
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm
f
x
x
2
−
2
x
,
∀
x
∈
ℝ
.
Hàm số
y
−
2
f
x
đồng biến trên khoảng ? A.
0
;
2
.
B.
−
2...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f ' x = x 2 − 2 x , ∀ x ∈ ℝ . Hàm số y = − 2 f x đồng biến trên khoảng ?
A. 0 ; 2 .
B. − 2 ; 0 .
C. 2 ; + ∞ .
D. − ∞ ; − 2 .
Đáp án A.
y ' = − 2 f ' x > 0 ⇔ f ' x < 0 ⇔ x 2 − 2 x < 0 ⇔ 0 < x < 2.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm
f
x
x
2
−
2
x
,
∀
x
∈
ℝ
.
Hàm số
y
−
2
f
x
đồng biến trên khoảng A. (0;2) B. (-2;0) C.
2
;
+
∞
D. ...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f ' x = x 2 − 2 x , ∀ x ∈ ℝ . Hàm số y = − 2 f x đồng biến trên khoảng
A. (0;2)
B. (-2;0)
C. 2 ; + ∞
D. - ∞ ; - 2
Cho hàm số f(x) liên tục trên
ℝ
có f(0)0 và đồ thị hàm số
y
f
(
x
)
như hình vẽ bênHàm số
y
3
f
(
x
)
-
x
3
đồng biến trên khoảng A.
2...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ có f(0)=0 và đồ thị hàm số y = f ' ( x ) như hình vẽ bên
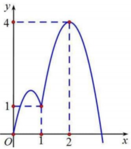
Hàm số y = 3 f ( x ) - x 3 đồng biến trên khoảng
A. 2 ; + ∞
B. - ∞ ; 2
C. (2;0)
D. (1;3)
Đặt g ( x ) = 3 f ( x ) - x 3 . Hàm số ban đầu có dạng y=|g(x)|
Ta có g ' ( x ) = 3 f ' ( x ) - 3 x 2 .
Cho g'(x)=0 ⇔ [ x = 0 x = 1 x = 2

Dễ thấy g(0)=0. Ta có bảng biến thiên
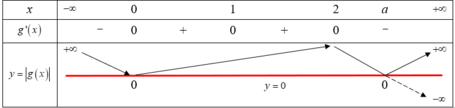
Dựa vào BBT suy ra hàm số y=|g(x)| đồng biến trên khoảng (0;2) và a ; + ∞ với g(a)=0
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm
f
x
x
2
x
2
-
1
,
∀
x
∈
ℝ
. Hàm số
y
2
f
-
x
đồng biến trên khoảng A.
2
;...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f ' x = x 2 x 2 - 1 , ∀ x ∈ ℝ . Hàm số y = 2 f - x đồng biến trên khoảng
A. 2 ; + ∞
B. - ∞ ; - 1
C. (-1;1)
D. (0;2)