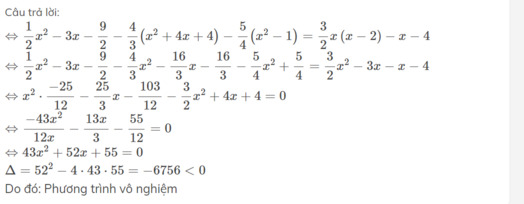Tìm x, biết:
(x.1)(x.x)=8
12(x+3)=60
\(\left(108.\frac{1}{2}\right)\left(6\div x\right)+123=231\)
\(x.x.\frac{1}{2}=100.2\)
\(\left(x+1\right)+\left(x+2\right)+...+\left(x+x\right)=8475\)
11321-8192+x=248.321
\(987654321-x.\frac{1}{2}=887654321\)
91930-x.2=89882