cho số thực dương a và b thoả mãn a100+b100 = a101+b101=a102+b102
tính a2022+b2023
Cho các số thực dương a và b thỏa mãn:
a100 + b100 = a101 + b101 = a102 + b102
Hãy tính giá trị biểu thức: P = a2004 + b2004
Ta có: \(\left(a^{100}+b^{100}\right)\cdot ab=a^{101}\cdot b+b^{101}\cdot a\)
\(\left(a^{101}+b^{101}\right)\cdot\left(a+b\right)=a^{102}+a^{101}\cdot b+b^{101}\cdot a+b^{102}\)
Do đó: \(\left(a^{101}+b^{101}\right)\left(a+b\right)-\left(a^{100}+b^{100}\right)\cdot ab\)
\(=a^{102}+b\cdot a^{101}+a\cdot b^{101}+b^{102}-a^{101}\cdot b-b^{101}\cdot a\)
\(=a^{102}+b^{102}\)
Kết hợp đề bài, ta có:
\(\left(a^{102}+b^{102}\right)\left(a+b\right)-\left(a^{102}+b^{102}\right)\cdot ab=a^{102}+b^{102}\)
\(\Leftrightarrow a+b-ab=1\)
\(\Leftrightarrow a+b-ab-1=0\)
\(\Leftrightarrow\left(a-1\right)+b\left(1-a\right)=0\)
\(\Leftrightarrow\left(a-1\right)-b\left(a-1\right)=0\)
\(\Leftrightarrow\left(a-1\right)\left(1-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-1=0\\1-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
Vậy: \(P=a^{2004}+b^{2004}=1^{2004}+1^{2004}=2\)
cho các số dương a và b thõa mãn điều kiện a100+b100=a101+b101=a102+b102 .Cmr : a+b/ab=a2+b2/ab
\(a^{100}+b^{100}=a^{101}+b^{101}=a^{102}+b^{102}\)
\(\Rightarrow\left(a^{100}+b^{100}\right)\left(a^{102}+b^{102}\right)=\left(a^{101}+b^{101}\right)^2\)
\(\Rightarrow a^{202}+b^{202}+a^{100}b^{102}+a^{102}b^{100}=a^{202}+b^{202}+2a^{101}b^{101}\)
\(\Rightarrow a^{100}b^{100}\left(a^2+b^2\right)=a^{100}b^{100}\left(2ab\right)\)
\(\Rightarrow a^2+b^2=2ab\)
\(\Rightarrow\left(a-b\right)^2=0\)
\(\Rightarrow a=b\)
Thế vào \(a^{100}+b^{100}=a^{101}+b^{101}\)
\(\Rightarrow a^{100}+a^{100}=a^{101}+a^{101}\)
\(\Rightarrow2a^{100}\left(a-1\right)=0\)
\(\Rightarrow a=1\Rightarrow b=1\)
\(\Rightarrow...\)
Cho các số dương a và b thỏa mãn điều kiện: a100+b100=a101+b101=a102+b102 Chứng minh rằng: a+b/ab=a^2+b^2/a^2b^2
abab-baba chia hết cho 101
=a1000+b100+a10+b-b1000+a100+b10+a
=a1010+b101-b1010+a101
=a(1010+101)-b(101-1010)
Như vậy có đúng không ạ chỉ cần check đúng hoặc sai hộ tớ thui nhea nhanh tớ tick nhé.
dòng thứ 2 bạn phải đóng ngoặc chứ
sửa lại:
=a1000+b100+a10+b-(b1000+a100+b10+a)
Cảm ơn bạn nhé vậy là mình làm sai rùi.
a,cho a1 +a2+a3+.....+a101=0 và a1 +a2= a3+a4=.....=a99+a100=-1
Tìm a101
b,tìm số nguyên a biết
-2017</a+4/< hoặc = 2
a.
Theo đề bài ta có:
-1 - 1 - ... - 1 + a101 = 0
=> - 50 + a101 = 0=> a101 = 50
b,
-2017 < |a+4| ≤ 2
=> 0 ≤ |a+4| ≤ 2
=> -2 ≤ a+4 ≤ 2
=> -6 ≤ a ≤ -2
Cho A1,A2,A3,A4,.....,A100 là các số nguyên thoả mãn A1+A2+A3+....+A100=2*2019
Chứng minh rằng : A1*2+A2*2+A3*2+.…..+A100*2 chia hết cho 2
\(A_1+A_2+A_3+...+A_{100}=2.2019\). Mà 2.2019 chia hết cho 2
\(\Rightarrow A_1+A_2+A_3+...+A_{100}⋮2\)
\(\Rightarrow A_1.2+A_2.2+A_3.2+...+A_{100}.2\)
\(=2.\left(A_1+A_2+A_3+...+A_{100}\right)⋮2\)
=> 2(A1+A2+A3+....+A100)
Mà 2 chia hết cho 2
=> 2(A1+A2+A3+....+A100) chia hết cho 2
=> A1.2+A2.2+A3.2+.…..+A100.2 chia hết cho 2(đpcm)
Ta luôn luôn có :
n²-n=n.n-n=n×(n-1)
Nxét:n và n-1 là 2 số tự nhiên liên tiếp⇒n×(n-1)⋮ 2 (1)
\(\Rightarrow S=a\dfrac{2}{1}+a\dfrac{2}{2}+a\dfrac{2}{3}+...+a-\left(a_1+a_2+a_3+...+a_{100}\right)\\ \Rightarrow S=a\dfrac{2}{1}+a\dfrac{2}{2}+a\dfrac{2}{3}+...+a\dfrac{2}{100}-\left(a_1-a_2-a_3-...-a_{100}\right)\\ \Rightarrow S=\left(a\dfrac{2}{1}-a_1\right)+\left(a\dfrac{2}{2}-a_2\right)+\left(a\dfrac{2}{3}-a_3\right)+...\left(a\dfrac{2}{100}-a_{100}\right)⋮2\)
\(\Rightarrow a\dfrac{2}{1}+a\dfrac{2}{2}+a\dfrac{2}{3}+...+a\dfrac{2}{100}⋮2\)
cho a,b dương và a2020 + b2020 = a2021 + b2021 = a2022 + b2022. tính a2025 + b2025
Cho hai số thực dương a,b thoả mãn a+b = 2018 và ∫ a b x x + 2018 - x d x = 10 Tích phân ∫ a b sin πx 3 d x bằng
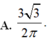
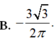
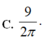
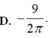
Cho hai số thực dương a,b thoả mãn a + b = 2018 và ∫ a b x x + 2018 - x d x = 10 Tích phân ∫ a b sin π x 3 d x bằng
A. 3 3 2 π
B. - 3 3 2 π
C. 9 2 π
D. - 9 2 π