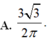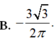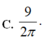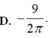Các câu hỏi tương tự
hàm số
f
(
x
)
ln
1
-
1
x
2
. Biết rằng
f
(
2
)
+
F
(
3
)
+
.
.
.
+
f
(
2018
)
ln
a
-
ln
b...
Đọc tiếp
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
Cho a,b là các số thực dương thỏa mãn
∫
a
b
f
(
x
)
d
x
1
. Tích phân
I
∫
ln
x
ln
b
e
x
.
f
e
x
c...
Đọc tiếp
Cho a,b là các số thực dương thỏa mãn ∫ a b f ( x ) d x = 1 . Tích phân I = ∫ ln x ln b e x . f e x có giá trị bằng bao nhiêu?
A. I = 0.
B. I = 1.
C. I = |a-b|.
D. I = e.
Gọi x và y là các số thực dương thỏa mãn điều kiện
log
9
x
log
6
y
log
4
(
x
+
y
)
và
x
y
-
a
+
b
2
với a, b là hai số nguyên dương. Tính...
Đọc tiếp
Gọi x và y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính T = a + b
A. T=6
B. T=4
C. T=11
D. T=8
Gọi x, y là các số thực dương thỏa mãn
log
9
x
log
6
y
log
4
(
x
+
y
)
và
x
y
-
a
+
b
2
với a...
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính tổng T = a+b
A. T = 6
B. T = 4
C. T = 11
D. T = 8
Cho các số thực dương a,b, x thoả mãn
log
1
/
2
x
2
3
log
1
/
2
a
-
1
5
log
1
/
2...
Đọc tiếp
Cho các số thực dương a,b, x thoả mãn log 1 / 2 x = 2 3 log 1 / 2 a - 1 5 log 1 / 2 b . Mệnh đề nào dưới đây đúng ?
A.![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
với a0, c2018 và a+b+c2018. Số điểm cực trị của hàm số
y
f
(
x
)
-
2018
là A. 1 B. 3 C. 5 D. 7
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c với a>0, c>2018 và a+b+c<2018. Số điểm cực trị của hàm số y = f ( x ) - 2018 là
A. 1
B. 3
C. 5
D. 7
Biết
a
b
(trong đó
a
b
là phân số tối giản,
a
,
b
∈
N
*
) là giá trị thực của tham số m để hàm số
y
2
x
3
-
3
m
x
2
-
6
(
3
m
2...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản, a , b ∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 m x 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P=a+2b.
![]()
![]()
![]()
Cho hàm số y f( x) đạo hàm f’ (x) -x2- 1. Với các số thực dương a, b thỏa mãn a b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng A. f(a) B.
f
a
b
C. f( b) D.
f
a
+
b
2
Đọc tiếp
Cho hàm số y= f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a< b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
A. f(a)
B. f a b
C. f( b)
D. f a + b 2