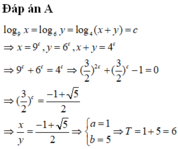Các câu hỏi tương tự
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
P
log
(
a
2
b
3
)
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Gọi x và y là các số thực dương thỏa mãn điều kiện
log
9
x
log
6
y
log
4
(
x
+
y
)
và
x
y
-
a
+
b
2
với a, b là hai số nguyên dương. Tính...
Đọc tiếp
Gọi x và y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính T = a + b
A. T=6
B. T=4
C. T=11
D. T=8
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Gọi x, y là các số thực dương thỏa mãn điều kiện
log
9
x
log
6
y
log
4
(
x
+
y
)
và
x
y
-
a
+
b
2
, với a, b là hai số nguyên dương. Tính a.b.
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 , với a, b là hai số nguyên dương. Tính a.b.
![]()
![]()
![]()
![]()
Gọi x, y là các số thực dương thỏa mãn điều kiện log9 x log6 x log4 (x + y) và biết rằng
x
y
-
a
+
b
2
với a, b là các số nguyên dương. Tính giá trị a + b. A. a + b 6 B. a + b 11 C. a + b 4 D. a + b 8
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn điều kiện log9 x = log6 x = log4 (x + y) và biết rằng x y = - a + b 2 với a, b là các số nguyên dương. Tính giá trị a + b.
A. a + b = 6
B. a + b = 11
C. a + b = 4
D. a + b = 8
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho hai số thực
x
,
y
thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
(
11
-
2
x
-
y
)
2
x
+
4
y
-
1
...
Đọc tiếp
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho hai số dương a và b. Đặt
X
log
a
+
b
2
,
Y
log
a
+
log
b
2
. Khẳng định nào dưới đây là đúng
Đọc tiếp
Cho hai số dương a và b. Đặt X = log a + b 2 , Y = log a + log b 2 . Khẳng định nào dưới đây là đúng
![]()
![]()
![]()
![]()