Rút gọn biểu thức: (sina + cosa)² - 2sina.cosa

Những câu hỏi liên quan
Rút gọn biểu thức P=(1-sina+cosa)/(1-sina-cosa)
[1-2sina/2cosa/2+(2cos^2a/2 - 1)]/[1-2sina/2cosa/2-1+2sin^a]
=2cosa/2(cosa/2-sina/2)/[2sina/2(sina/2-cosa/2)]
= -cota/2
Đúng 0
Bình luận (0)
Rút gọn: \(\dfrac{sina+cosa-1}{sina-cosa+1}\)
Rút gọn biểu thức: a)\(\left(1+tanA+\frac{1}{cosA}\right)\left(1+tanA-\frac{1}{cosA}\right)\)
b) \(\sqrt{\frac{1+sinA}{1-sinA}+\sqrt{\frac{1-sinA}{1+sinA}}}\).
Rút gọn biểu thức :
C\(=\frac{\sqrt{2}-sina-cosa}{sina-cosa}\)
Chứng minh biểu thức sau
Cosa / 1-sina = 1+ sina/cosa
VT=\(\dfrac{c\text{os}a}{1-sina}\)
\(=\dfrac{c\text{os}a\left(1+sina\right)}{\left(1-sina\right)\left(1+sina\right)}=\dfrac{c\text{os}a\left(1+sina\right)}{1-sin^2a}\\ \\ \\ =\dfrac{c\text{os}a\left(1+sina\right)}{c\text{os}^2a}=\dfrac{1+sina}{c\text{os}a}=VP\left(\text{đ}pcm\right)\)
Đúng 0
Bình luận (0)
Mn giúp mình câu này với
tana - 3cota=6 và π < α < \(\dfrac{3\Pi}{2}\)
a/ A= sina+cosa
b/ B= 2Sina.cosa
c/ C= \(\dfrac{2sina-tana}{cosa+cota}\)
Đề: Rút gọn biểu thức sau: D= (1+ cosa + cos 2a + cos 3a)/ (cosa + 2 cos ²a - 1)
Lời giải:
$D=\frac{1+\cos a+2\cos ^2a-1+4\cos ^3a-3\cos a}{\cos a+2\cos ^2a-1}$
$=\frac{4\cos ^3a+2\cos ^2a-2\cos a}{\cos a+2\cos ^2a-1}$
$=\frac{2\cos a(\cos a+2\cos ^2a-1)}{\cos a+2\cos ^2a-1}$
$=2\cos a$
Đúng 1
Bình luận (0)
Chứng minh đẳng thức sau:Sina/Sina - cosa - cosa/cosa- Sina = 1+ cot²a/1-cot²a
\(\dfrac{sina}{sina-cosa}-\dfrac{cosa}{cosa-sina}=\dfrac{sina+cosa}{sina-cosa}=\dfrac{1+cota}{1-cota}=\dfrac{\left(1+cota\right)^2}{1-cot^2a}\)
Đề bài ko đúng
Đúng 0
Bình luận (0)
Đơn giản biểu thức
A
cos
a
-
π
2
+
sin
a
-
π
ta được: A. A cos + sina B. A 2sina C. A 0 D. Tất cả sai
Đọc tiếp
Đơn giản biểu thức A = cos a - π 2 + sin a - π ta được:
A. A = cos + sina
B. A = 2sina
C. A = 0
D. Tất cả sai
Chọn C.
Do hai góc phụ nhau thì sin góc này bằng cos góc kia; hai góc bù nhau thì sin bằng nhau nên ta có:
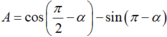
Hay A= sin α - sinα = 0.
Đúng 0
Bình luận (0)
















