Tìm tập xác định
a. y= 3/sinx - 4/cosx
b. tanx- cotx

Những câu hỏi liên quan
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
1. cho 180 độ x 250 độ. kết quả đúng làA. sinx0, cosx0B. sinx0, cosx0C. sinx0, cosx0D. sinx0, cosx02. cho dfrac{3pi}{4} x dfrac{3pi}{2} kết quả đúng làA. tanx0, cotx0B. tanx0, cotx0C. tanx0, cotx0D. tanx0, cotx03. cho 2pi x dfrac{5pi}{2} kết quả đúng làA. tanx0, cotx0B. tanx0, cotx0C. tanx0, cotx0D. tanx0, cotx04. cho 630 độ x 720 độ. kết quả đúng làA. sinx0, cosx0B. sinx0, cosx0C. sinx0, cosx0D. sinx0, cosx0
Đọc tiếp
1. cho 180 độ < x < 250 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
2. cho \(\dfrac{3\pi}{4}\) <x< \(\dfrac{3\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
3.
cho 2\(\pi\) < x <\(\dfrac{5\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
4.
cho 630 độ < x <720 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
tìm tập xác định của hàm số sau:
a, y=cot \(\left(\frac{\pi}{2}.sinx\right)\)
b, y= \(\sqrt{sinx-1}+2-cos^2x\)
c, y= \(\frac{tanx+cotx}{cos2x}\)
d, y=\(\frac{sinx-tanx}{sinx+cotx}\)
e, y=\(\frac{cotx}{cos^2x-3cosx+2}\)
a/ ĐKXĐ:
\(sin\left(\frac{\pi}{2}.sinx\right)\ne0\Rightarrow\frac{\pi}{2}.sinx\ne k\pi\)
\(\Rightarrow sinx\ne2k\)
Mà \(-1\le sinx\le1\Rightarrow sinx\ne0\Rightarrow x\ne k\pi\)
b/
\(sinx-1\ge0\Leftrightarrow sinx\ge1\Rightarrow sinx=1\)
\(\Rightarrow x=\frac{\pi}{2}+k2\pi\)
c/
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cos2x\ne0\end{matrix}\right.\) \(\Rightarrow sin4x\ne0\)
\(\Rightarrow x\ne\frac{k\pi}{4}\)
d/
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\sinx+cotx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\sin^2x+cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne k\pi\\-cos^2x+cosx+1\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\cosx\ne\frac{1-\sqrt{5}}{2}\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\pm arccos\left(\frac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\)
e/
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sinx\ne0\Rightarrow x\ne k\pi\)
Đúng 0
Bình luận (0)
tìm tập xác định của y=sinx+1/sinx ạ và y=sin2x+cosx/tanx-sinx ạ
\(y=\dfrac{sinx+1}{sinx}\)
ĐKXĐ: \(sinx\ne0\Rightarrow x\ne k\pi\)
\(y=\dfrac{sin2x+cosx}{tanx-sinx}\)
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\left(\dfrac{1}{cosx}-1\right)\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\)
\(\Rightarrow sin2x\ne0\)
\(\Rightarrow x\ne\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
tìm đạo hàm cấp n của hàm y=cosx; y=tanx; y=cotx; y=sinx.
\(y=sinx\Rightarrow y'=cosx;y''=-sinx;y'''=-cosx\)
Bằng quy nạp toán học ; ta c/m được : \(y^{\left(n\right)}sinx=sin\left(x+n\dfrac{\pi}{2}\right)\)
Đúng 2
Bình luận (0)
1. Cho sinx=-3/5 , x thuộc (-π/2 , 0) . Tính A= sinx + 6 cosx -3 tanx .
2. Cho cotx = 3 . Tính B=5sinx + 3cosx / 3cosx - 2sinx
3. Cho cosx=2/3 . Tính C= cotx-2tanx / 5cotx + tanx
4. Chứng minh ;
Cosx/ 1+ sinx +tanx = 1/ cosx
a/ \(cosx>0\Rightarrow cosx=\sqrt{1-sin^2x}=\frac{4}{5}\)
\(\Rightarrow tanx=-\frac{3}{4}\Rightarrow A=\frac{129}{20}\)
b/ \(B=\frac{5sinx+3cosx}{3cosx-2sinx}=\frac{\frac{5sinx}{sinx}+\frac{3cosx}{sinx}}{\frac{3cosx}{sinx}-\frac{2sinx}{sinx}}=\frac{5+3cotx}{3cotx-2}=\frac{5+9}{9-2}\)
c/ \(C=\frac{sinx.cosx\left(cotx-2tanx\right)}{sinx.cosx\left(5cotx+tanx\right)}=\frac{cos^2x-2sin^2x}{5cos^2x+sin^2x}=\frac{cos^2x-2\left(1-cos^2x\right)}{5cos^2x+1-cos^2x}=\frac{3cos^2x-2}{4cos^2x+1}=...\)
d/ Không dịch được đề, ko biết mẫu số bên trái nó đến đâu cả
tìm tập xác định y = sin^2x - 3sinx / (tanx -1 ) (cotx + 1) giúp mình với ạ
Hàm là vậy phải không nhỉ? \(y=\dfrac{sin^2x-3sinx}{\left(tanx-1\right)\left(cotx+1\right)}\)
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\tanx-1\ne0\\cotx+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne1\\cotx\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{4}\)
Đúng 2
Bình luận (1)
Tìm giá trị nhỏ nhất của hàm số
y
sin
x
+
cos
x
+
tan
x
+
c
o
t
x
+
1...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = sin x + cos x + tan x + c o t x + 1 sin x + 1 cos x
A. 2 2 - 1
B. 2 + 1
C. 2 2 + 1
D. 2 - 1
Đáp án A
Phương pháp: Đặt sinx = a, cosx = b
Cách giải: Đặt sinx = a, cosx = b ta có a2 + b2 = 1
Khi đó 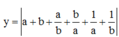
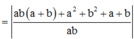
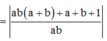
Đặt 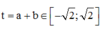
![]()
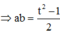
khi đó ta có : 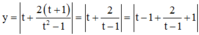
Nếu 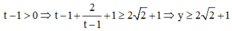
Nếu ![]()
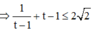
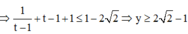
Vậy ![]()
Dấu bằng xảy ra ![]()
![]()
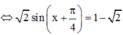
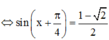
Đúng 0
Bình luận (0)
tanx-3.cotx= 4.(sinx+√3.cosx)


















