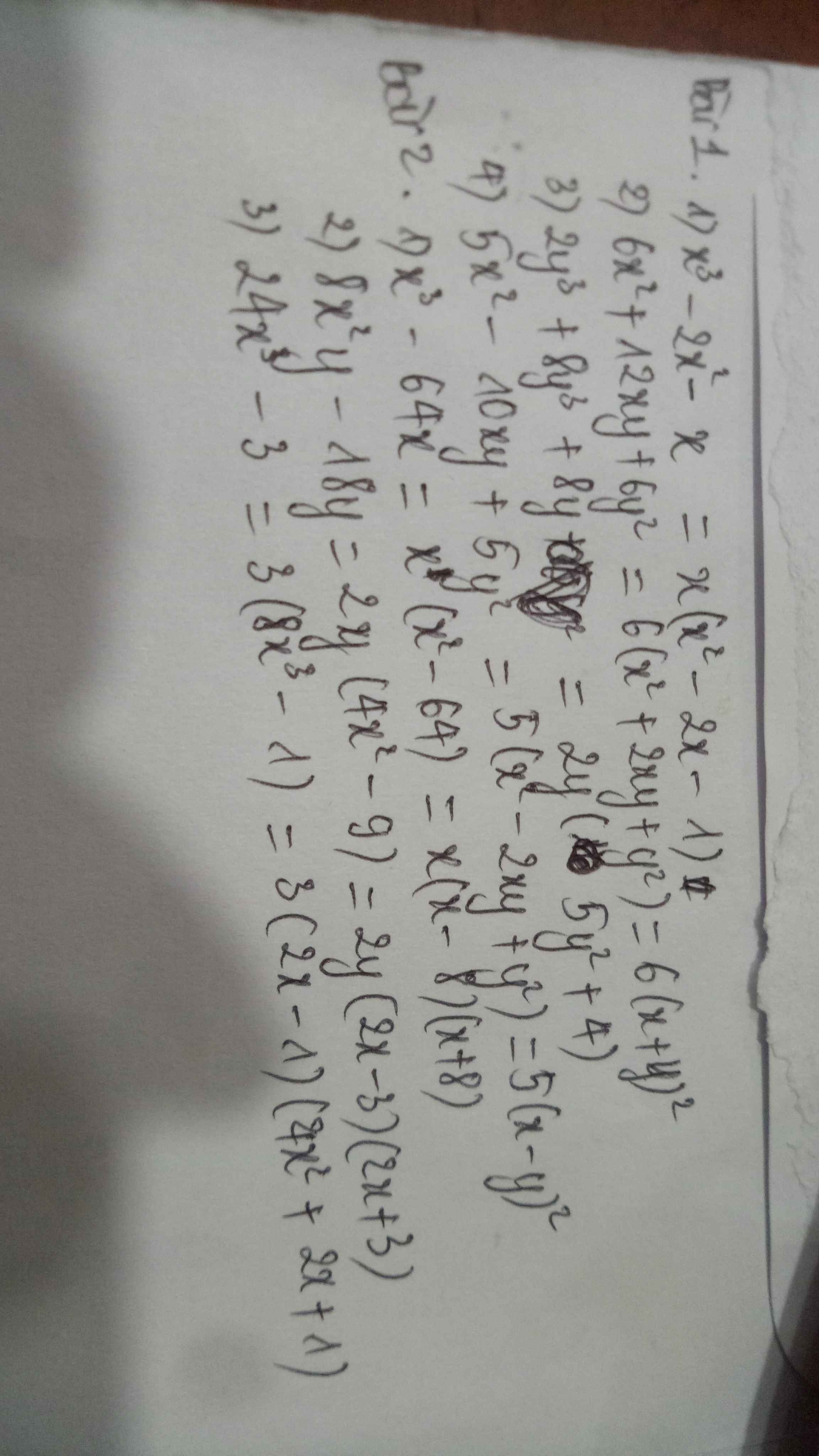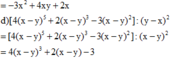6x2 - 12xy + 6y2 - 6x2

Những câu hỏi liên quan
Bài 1: Phân tích các đa thức sau thành nhân tử HD: Dùng phương pháp đặt nhân tử chung phối hợp dùng hằng đẳng thức số 1, 2 1) x3 – 2x – x 2) 6x2 + 12xy + 6y2 3) 2y3 + 8y3 + 8y 4) 5x2 – 10xy + 5y2 Bài 2: Phân tích các đa thức sau thành nhân tử HD: Dùng pp đặt nhân tử chung phối hợp dùng hằng đẳng thức số 3, 6, 7 1) x3 – 64x 2) 8x2y – 18y 3) 24x3 – 3 Bài 3: Phân tích các đa thức sau thành nhân tử HD: Dùng phương pháp nhóm hạng tử phối hợp dùng hằng đẳng thức 1) 5x2 + 10x +...
Đọc tiếp
Bài 1: Phân tích các đa thức sau thành nhân tử
HD: Dùng phương pháp đặt nhân tử chung phối hợp dùng hằng đẳng thức số 1, 2
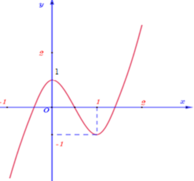
1) x3 – 2x – x 2) 6x2 + 12xy + 6y2
3) 2y3 + 8y3 + 8y 4) 5x2 – 10xy + 5y2
Bài 2: Phân tích các đa thức sau thành nhân tử
HD: Dùng pp đặt nhân tử chung phối hợp dùng hằng đẳng thức số 3, 6, 7
1) x3 – 64x 2) 8x2y – 18y 3) 24x3 – 3
Bài 3: Phân tích các đa thức sau thành nhân tử
HD: Dùng phương pháp nhóm hạng tử phối hợp dùng hằng đẳng thức
1) 5x2 + 10x + 5 – 5y2 2) 3x3 – 6x2 + 3x – 12xy2
3) a3b – ab3 + a2 + 2ab + b2 4) 2x3 – 2xy2 – 8x2 + 8xy
Giup mik với mik cần gấp lắm!
Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)
Đúng 1
Bình luận (0)
Bài 1;
1) \(x^3-2x-x=x\left(x^2-2x-1\right)\)
2) \(6x^2+12xy+6y^2=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\)
3) \(2y^3+8y^3+8y=10y^3+8y=2y\left(5y^2+4\right)\)
4) \(5x^2-10xy+5y^2=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
1) \(x^3-64x=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\)
2) \(8x^2y-18y=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\)
3) \(24x^3-3=3\left(8x^3-1\right)=3\left(2x-1\right)\left(4x^2+2x+1\right)\)
Bài 3:
1) \(5x^2+10x+5-5y^2=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y\right]=5\left(x-y+1\right)\left(x+y+1\right)\)
2) \(3x^3-6x^2+3x-12xy^2=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=3x\left(x-2y-1\right)\left(x+2y-1\right)\)
3) \(a^3b-ab^3+a^2+2ab+b^2=ab\left(a^2-b^2\right)+\left(a+b\right)^2=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2=\left(a+b\right)\left(a^2b-ab^2+a+b\right)\)
4) \(2x^3-2xy^2-8x^2+8xy=2x\left(x^2-y^2-4x+4y\right)=2x\left[\left(x-y\right)\left(x+y\right)-4\left(x-y\right)\right]=2x\left(x-y\right)\left(x+y-4\right)\)
Đúng 1
Bình luận (0)
Tính giá trị biểu thức : (2xy2 - 5y3) : y2 + (12xy + 6x2) : 3x tại x= -3 ; y= -12
\(\left(2xy^2-5y^3\right):y^2+\left(12xy+6x^2\right):3x\)
\(=\dfrac{y^2\left(2x-5y\right)}{y^2}+\dfrac{3x\left(4y+2x\right)}{3x}\)
\(=2x-5y+4y+2x\)
\(=4x-y\)
Thay x=-3, y=-12 vào biểu thức ta có:
\(4\cdot-3-\left(-12\right)=0\)
Vậy: ...
Đúng 3
Bình luận (0)
\(A=\dfrac{2xy^2-5y^3}{5y}+\dfrac{12xy+6x^2}{3x}\)
=2/5xy-y^2+4y+2x
Khi x=-3 và y=-12 thì A=2/5*(-3)*(-12)-144+4*(-12)+2*(-3)
=-183,6
Đúng 1
Bình luận (1)
tính
a, 6x2(3x2 - 4x + 5)
b, ( x - 2y ) ( 3xy + 6y2 +x)
c, ( 18x4y3 - 24x3y4 + 12x3y3 ) : ( -6x2y3 )
d, [4( x - y )5 + 2( x - y )3 - 3( x-y )2 ] : ( y - x )2
\(a,=18x^4-24x^3+30x\\ b,=3x^2y+6xy^2+x^2-6xy^2-12y^3-2xy=3x^2y+x^2-12y^3-2xy\\ c,=-3x^2+4xy-2x\\ d,=\left(x-y\right)^2\left[4\left(x-y\right)^3+2\left(x-y\right)-3\right]:\left(x-y\right)^2\\ =4\left(x-y\right)^3+2\left(x-y\right)-3\)
Đúng 1
Bình luận (0)
a: \(=18x^4-24x^3+30x^2\)
b: \(=3x^2y+6xy^2+x^2-6xy^2-12y^3-2xy\)
\(=x^2-12y^3+3x^2y-2xy\)
Đúng 0
Bình luận (0)
a, \(=18x^4-24x^3+30x^2\)
b, \(=3x^2y+6xy^2+x^2-6xy^2-12y^3-2xy=3x^2y+x^2-12y^3-2xy\)
c, \(=-3x^2+4xy-2x\)
d, \(=4\left(x-y\right)^3+2\left(x-y\right)-3=4\left(x^3-3x^2y+3xy^2-y^3\right)+2x-2y-3=4x^3-12x^2y+12xy^2-4y^3+2x-2y-3\)
Đúng 0
Bình luận (0)
Tính:a)
6
x
2
(
3
x
2
–
4
x
+
5
)
b)
(
x
-
2
y
)
(
3
x
y
+
6
y
2
+
x
)
c)
(
18
x
4
y
3
–...
Đọc tiếp
Tính:
a) 6 x 2 ( 3 x 2 – 4 x + 5 )
b) ( x - 2 y ) ( 3 x y + 6 y 2 + x )
c) ( 18 x 4 y 3 – 24 x 3 y 4 + 12 x 3 y 3 ) : ( - 6 x 2 y 3 )
d) [ 4 ( x – y ) 5 + 2 ( x – y ) 3 – 3 ( x – y ) 2 ] : ( y – x ) 2
Bài 3: Phân tích đa thức sau thành nhân tử.
a) x4 + 2x2 + 1
b) 4x2 - 12xy + 9y2
c) -x2 - 2xy - y2
d) (x + y)2 - 2(x + y) + 1
e) x3 - 3x2 + 3x - 1
g) x3 + 6x2 + 12x + 8
h) x3 + 1 - x2 - x
k) (x + y)3 - x3 - y3
a) x⁴ + 2x² + 1
= (x²)² + 2.x².1 + 1²
= (x² + 1)²
b) 4x² - 12xy + 9y²
= (2x)² - 2.2x.3y + (3y)²
= (2x - 3y)²
c) -x² - 2xy - y²
= -(x² + 2xy + y²)
= -(x + y)²
d) (x + y)² - 2(x + y) + 1
= (x + y)² - 2.(x + y).1 + 1²
= (x - y + 1)²
Đúng 2
Bình luận (0)
e) x³ - 3x² + 3x - 1
= x³ - 3.x².1 + 3.x.1² - 1³
= (x - 1)³
g) x³ + 6x² + 12x + 8
= x³ + 3.x².2 + 3.x.2² + 2³
= (x + 2)³
h) x³ + 1 - x² - x
= (x³ + 1) - (x² + x)
= (x + 1)(x² - x + 1) - x(x + 1)
= (x + 1)(x² - x + 1 - x)
= (x + 1)(x² - 2x + 1)
= (x + 1)(x - 1)²
k) (x + y)³ - x³ - y³
= (x + y)³ - (x³ + y³)
= (x + y)³ - (x + y)(x² - xy + y²)
= (x + y)[(x + y)² - x² + xy - y²]
= (x + y)(x² + 2xy + y² - x² + xy - y²)
= (x + y).3xy
= 3xy(x + y)
Đúng 0
Bình luận (0)
Câu 1: Chọn câu trả lời đúng: (3x2 – 5x + 2) + (3x2 + 5x) = A. 6x2 - 10x + 2 B. 6x2 +2 C. 6x2 + 2; D. 9x2 +2.
Đáp án: B hoặc C (Sao B và C lại giống nhau nhỉ ?!?)
\(3x^2-5x+2+3x^2+5x=\left(3x^2+3x^2\right)+\left(-5x+5x\right)+2=6x^2+2\)
(3x2-5x+2)+(3x2+5x)
=3x2-5x+2+3x2+5x
=6x2+2
=>Đáp án đúng là B và C
Cho hàm số
y
4
x
3
-
6
x
2
+
1
có đồ thị là đường cong trong hình dưới đây. Khi đó phương trình
4
4
x
3
-
6
x...
Đọc tiếp
Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
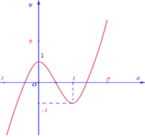
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
Cho hàm số
y
4
x
3
-
6
x
2
+
1
có đồ thị là đường cong trong hình dưới đây. Khi đó phương trình
4
4
x
3
-
6
x...
Đọc tiếp
Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
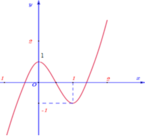
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 2 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
Đáp án C
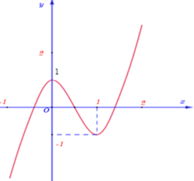

Vậy phương trình đã cho có 7 nghiệm thực.
Đúng 0
Bình luận (0)
a) (a2 - 1)2 + 4a2 = (a2 + 1)2
b) (6x2 + y2)(y2 - 6x2)
GIÚP MÌNH VỚI Ạ
a) (a2 - 1)2 + 4a2
= a4 - 2a2 + 1 + 4a2
= (a2)2 + 2.a2.1 + 12)
=(a2 + 1)2
b) (6x2 + y2)(y2 - 6x2)
= (y2 + 6x2)(y2 - 6x2)
= (y2)2 - (6x2)2
= y4 - 36x4
Đúng 1
Bình luận (0)