Giải phương trình lượng giác sau:
\(\dfrac{cos2x}{1-sinx}=0\)
Giải các phương trình sau:
a, \(\dfrac{Sin^2x+Sinx}{Sinx-1}=-2\)
b,\(\dfrac{Cos2x+Sinx}{Sinx-1}+1=0\)
a)Đk:\(sinx\ne1\)
Pt\(\Leftrightarrow sin^2x+sinx=-2\left(sinx-1\right)\)
\(\Leftrightarrow sin^2x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{-3+\sqrt{17}}{2}\left(tm\right)\\sinx=\dfrac{-3-\sqrt{17}}{2}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\\x=\pi-arc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\end{matrix}\right.\)(\(k\in Z\))
b)Đk:\(sinx\ne1\)
Pt \(\Leftrightarrow\dfrac{1-2sin^2x+sinx}{sinx-1}+1=0\)
\(\Leftrightarrow\dfrac{-\left(sinx-1\right)\left(2sinx+1\right)}{sinx-1}+1=0\)
\(\Leftrightarrow-\left(2sinx+1\right)+1=0\)
\(\Leftrightarrow sinx=0\) (tm)
\(\Leftrightarrow x=k\pi,k\in Z\)
Vậy...
giải phương trình sau:
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}\)=0
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)
\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)
\(\Leftrightarrow2cos^22x-2cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)
Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)
giải phương trình lượng giác
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
ĐK: \(x\ne\dfrac{\pi}{6}+k2\pi;x\ne\dfrac{5\pi}{6}+k2\pi\)
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=0\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đối chiếu điều kiện ta được \(x=-\dfrac{5\pi}{6}+k2\pi\).
Giải các phương trình sau cos2x - sinx - 1 = 0
cos 2 x - sin x - 1 = 0 ⇔ 1 - 2 sin 2 x - sin x - 1 = 0 ⇔ sin x ( 2 sin x + 1 ) = 0
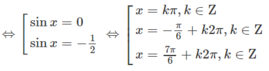
giải phương trình \(\dfrac{cos2x+3cosx+1}{sinx+1}=-1\)
@Nguyễn Việt Lâm anh giải bài này như nào ạ, cách của em nó dài mất hơn nữa mặt giấy '^^
ĐKXĐ: ...
\(\Leftrightarrow cos2x+3cosx+1=-sinx-1\)
\(\Leftrightarrow cos2x+3cosx+sinx+2=0\)
\(\Leftrightarrow cos^2x-sin^2x+3cosx+sinx+2=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx\right)+cosx-sinx+2cosx+2sinx+2=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx+1\right)+2\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow\left(cosx-sinx+2\right)\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow...\)
\(\dfrac{1+sinx+cosx}{cos2x-1}\)=\(2-tanx\)
giải phương trình
\(cos2x+2cosx-sin^2\dfrac{x}{2}=0\)
Giải phương trình lượng giác
\(\Leftrightarrow2cos^2x-1+2cosx-\left(\dfrac{1}{2}-\dfrac{1}{2}cosx\right)=0\)
\(\Leftrightarrow2cos^2x+\dfrac{5}{2}cosx-\dfrac{3}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{-5+\sqrt{73}}{8}\\cosx=\dfrac{-5-\sqrt{73}}{8}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm arccos\left(\dfrac{-5+\sqrt{73}}{8}\right)+k2\pi\)
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
Số điểm biểu diễn nghiệm của phương trình cos 2 x + sinxcosx + cosx − sinx = 0 trên đường tròn lượng giác là
A. 4
B. 2
C. 1
D. 3
Đáp án C
Nhận thấy cos x = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được
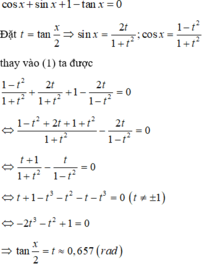
Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.