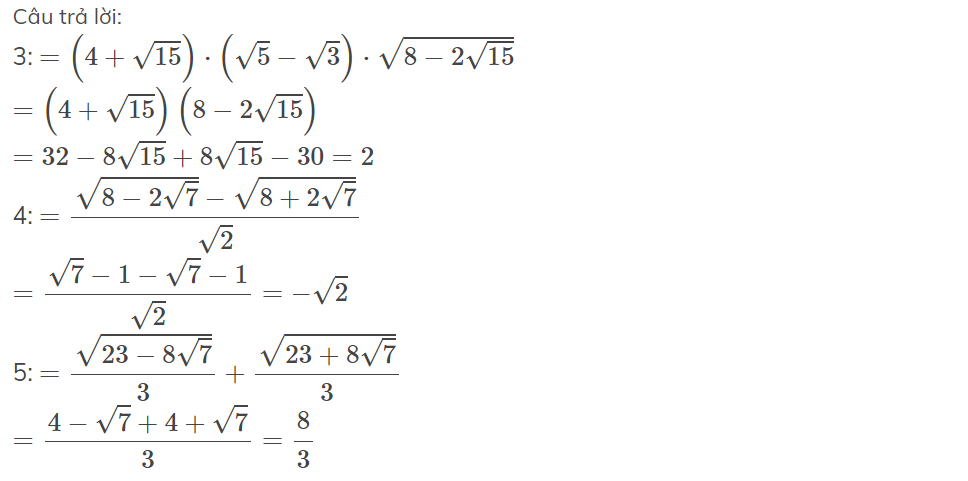a: =2-căn 3-2-căn 3

=-2căn 3

b: \(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8+2\sqrt{7}}-\sqrt{8-2\sqrt{7}}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}+1-\sqrt{7}+1\right)=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)

c: \(A=\sqrt{4-\sqrt{10-2\sqrt{5}}}-\sqrt{4+\sqrt{10-2\sqrt{5}}}\)

=>\(A^2=4-\sqrt{10-2\sqrt{5}}+4+\sqrt{10-2\sqrt{5}}+2\cdot\sqrt{16-10+2\sqrt{5}}\)

\(\Leftrightarrow A^2=8+2\left(\sqrt{5}+1\right)=10+2\sqrt{5}\)

=>\(A=\sqrt{10+2\sqrt{5}}\)

Ta có: 

\(R=\)\(\dfrac{3+\sqrt{5}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}+\dfrac{3-\sqrt{5}}{2\sqrt{2}-\sqrt{3-\sqrt{5}}}\)

\(=\)\(\dfrac{\sqrt{10}+3\sqrt{2}}{5+\sqrt{5}}+\dfrac{\sqrt{10}-3\sqrt{2}}{5-\sqrt{5}}\)

\(=\dfrac{4\sqrt{2}}{\sqrt{5}\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)

\(=\dfrac{4\sqrt{2}}{4\sqrt{5}}=\sqrt{\dfrac{2}{5}}\)

Làm câu S tương tự như này rồi đối chiếu kết quả nha

b) Ta có: \(\sqrt{\dfrac{3+\sqrt{5}}{3-\sqrt{5}}}+\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)

\(=\sqrt{\dfrac{\left(3+\sqrt{5}\right)^2}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}}+\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}}\)

\(=\dfrac{3+\sqrt{5}}{2}+\dfrac{3-\sqrt{5}}{2}\)

\(=\dfrac{3+3}{2}=\dfrac{6}{2}=3\)

\(A=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}=\sqrt{3+1+2\sqrt{3.1}}-\sqrt{3+1-2\sqrt{3.1}}\)

\(=\sqrt{(\sqrt{3}+1)^2}-\sqrt{(\sqrt{3}-1)^2}=|\sqrt{3}+1|-|\sqrt{3}-1|=2\)

\(B=\sqrt{4+5-2\sqrt{4.5}}+\sqrt{4+5+2\sqrt{4.5}}=\sqrt{(\sqrt{4}-\sqrt{5})^2}+\sqrt{(\sqrt{4}+\sqrt{5})^2}\)

\(=|\sqrt{4}-\sqrt{5}|+|\sqrt{4}+\sqrt{5}|=2\sqrt{5}\)

\(C\sqrt{2}=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}=\sqrt{7+1-2\sqrt{7.1}}-\sqrt{7+1+2\sqrt{7.1}}\)

\(=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}\)

\(=|\sqrt{7}-1|-|\sqrt{7}+1|=-2\Rightarrow C=-\sqrt{2}\)

----------------------------

\(7+4\sqrt{3}=(2+\sqrt{3})^2\Rightarrow 10\sqrt{7+4\sqrt{3}}=10(2+\sqrt{3})\)

\(\Rightarrow \sqrt{48-10\sqrt{7+4\sqrt{3}}}=\sqrt{28-10\sqrt{3}}=\sqrt{(5-\sqrt{3})^2}=5-\sqrt{3}\)

\(\Rightarrow 3+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}=3+5(5-\sqrt{3})=28-5\sqrt{3}\)

\(\Rightarrow D=\sqrt{5\sqrt{28-5\sqrt{3}}}\)

Cách 1:

\(E=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})\sqrt{8-2\sqrt{15}}\)

\(=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})\sqrt{(\sqrt{5}-\sqrt{3})^2}\)

\(=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})(\sqrt{5}-\sqrt{3})=(4+\sqrt{15})(8-2\sqrt{15})\)

\(=2(4+\sqrt{15})(4-\sqrt{15})=2(16-15)=2\)

Cách 2:

\(E^2=(4+\sqrt{15})^2(\sqrt{10}-\sqrt{6})^2(4-\sqrt{15})=(4+\sqrt{15})(4-\sqrt{15})(4+\sqrt{15}).(16-4\sqrt{15})\)

\(=(16-15)(4+\sqrt{15})(4-\sqrt{15}).4=(16-15)(16-15).4=4\)

Vì $E>0$ nên $E=2$

Ta có: \(A=\frac{-\left(\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\right)}{\sqrt{7-4\sqrt{3}}-\sqrt{7+4\sqrt{3}}}\)

\(=\frac{-\left(\sqrt{3-2\cdot\sqrt{3}\cdot2+4}+\sqrt{3+2\cdot\sqrt{3}\cdot2+4}\right)}{\sqrt{3-2\cdot\sqrt{3}\cdot2+4}-\sqrt{3+2\cdot\sqrt{3}\cdot2+4}}\)

\(=\frac{-\left(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(\sqrt{3}+2\right)^2}\right)}{\sqrt{\left(\sqrt{3}-2\right)^2}-\sqrt{\left(\sqrt{3}+2\right)^2}}\)

\(=\frac{-\left(\left|\sqrt{3}-2\right|+\left|\sqrt{3}+2\right|\right)}{\left|\sqrt{3}-2\right|-\left|\sqrt{3}+2\right|}\)

\(=\frac{-\left(2-\sqrt{3}+\sqrt{3}+2\right)}{2-\sqrt{3}-\sqrt{3}-2}\)

\(=\frac{-4}{-2\sqrt{3}}=\frac{2\sqrt{3}}{3}\)

1: \(\sqrt{3+\sqrt{5}}\cdot\sqrt{2}=\sqrt{6+2\sqrt{5}}=\sqrt{5}+1\)

3) \(\left(\sqrt{\dfrac{3}{4}}-\sqrt{3}+5\cdot\sqrt{\dfrac{4}{3}}\right)\cdot\sqrt{12}\)

\(=\left(\dfrac{\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{2}+5\cdot\dfrac{2}{\sqrt{3}}\right)\cdot\sqrt{12}\)

\(=\dfrac{17\sqrt{3}}{6}\cdot2\sqrt{3}\)

\(=\dfrac{34\cdot3}{6}=\dfrac{102}{6}=17\)

a) Ta có: \(\sqrt{3-2\sqrt{2}}-\sqrt{11+6\sqrt{2}}\)

\(=\sqrt{2}-1-3-\sqrt{2}\)

=-4

b) Ta có: \(\sqrt{4-2\sqrt{3}}-\sqrt{7-4\sqrt{3}}+\sqrt{19+8\sqrt{3}}\)

\(=\sqrt{3}-1-2+\sqrt{3}+4+\sqrt{3}\)

\(=3\sqrt{3}+1\)

c) Ta có: \(\sqrt{6-2\sqrt{5}}+\sqrt{9+4\sqrt{5}}-\sqrt{14-6\sqrt{5}}\)

\(=\sqrt{5}-1+\sqrt{5}-2-3+\sqrt{5}\)

\(=3\sqrt{5}-6\)

d) Ta có: \(\sqrt{11-4\sqrt{7}}+\sqrt{23-8\sqrt{7}}+\sqrt{\left(-2\right)^6}\)

\(=\sqrt{7}-2+4-\sqrt{7}+8\)

=10