 giu
giu

Những câu hỏi liên quan
 giú
giú
Giú
XI
1 more exciting
2 most boring
3 fathest
4 well
5 happier
6 worst
7 colder
8 most difficult
9 better
10 carefully
XII
1 C
2 C
3 B
4 A
5 A
6 B
9 A
10 C
9 B
Đúng 2
Bình luận (0)
Giú ạ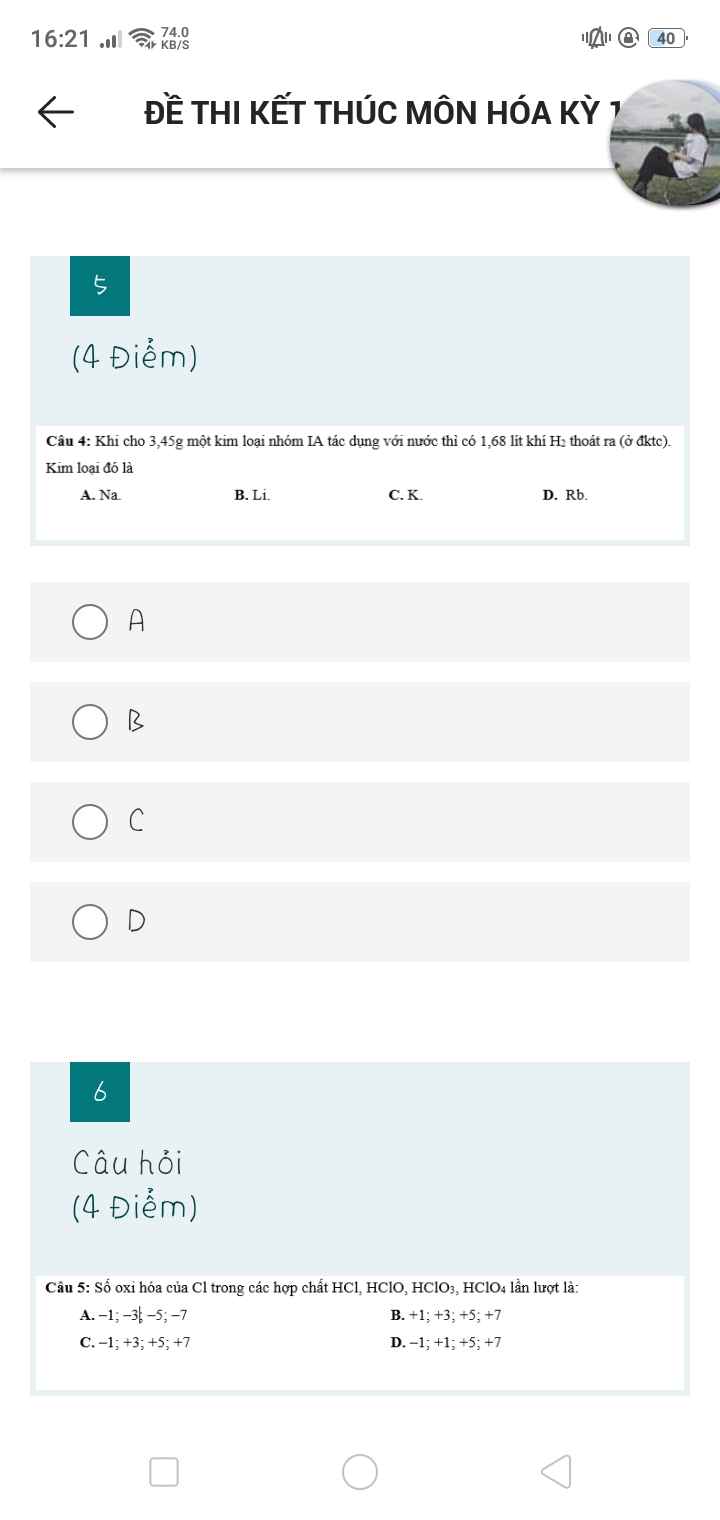
Câu 4 :
n H2 = 1,68/22,4 = 0,075(mol)
2R + 2HCl $\to$ 2RCl + H2
n R = 2n H2 = 0,15(mol)
=> M R = 3,45/0,15 = 23(Natri)
Câu 5 : D
Đúng 2
Bình luận (0)
Mn giú tui vs
Nhanh giú e ạ
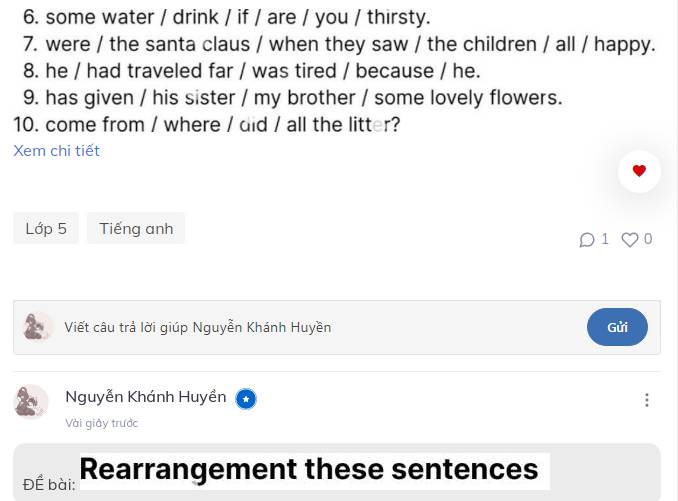
6 Drink some water if you are thirsty
7 The children were happy when they saw the Santa Clause
8 He was tired because he had traveled far
9 My brother has given his sister some lovely flowers
10 Where did all the litter come from?
Đúng 3
Bình luận (0)
 ecsresire 3 ạ giú mik
ecsresire 3 ạ giú mik
giú mk câu b với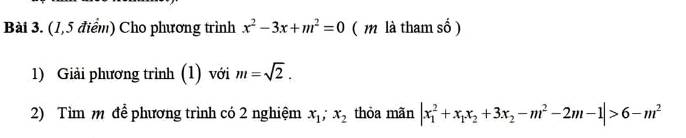
Lời giải:
Theo định lý Viet:
$x_1+x_2=3$
$x_1x_2=m^2$
Khi đó:
$|x_1^2+x_1x_2+3x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+x_1x_2+(x_1+x_2)x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+2x_1x_2+x_2^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |(x_1+x_2)^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |9-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |m^2+2m-8|> 6-m^2$
Nếu $m^2+2m-8\geq 0$ thì:
$m^2+2m-8> 6-m^2$
$\Leftrightarrow 2m^2+2m-14>0$
$\Leftrightarrow m^2+m-7>0$
$\Leftrightarrow m< \frac{-1-\sqrt{29}}{2}$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Kết hợp với $m^2+2m-8\geq 0$ suy ra $m\leq -4$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Nếu $m^2+2m-8<0$ thì:
$-(m^2+2m-8)> 6-m^2$
$\Leftrightarrow m< 1$
Kết hợp với $m^2+2m-8<0$ suy ra $-4< m< 1$
Vậy........
Đúng 0
Bình luận (0)
giú e bài 2 ạ\

Bài 2:
\(y=\left(\dfrac{2m-1}{-5m-10}\right)x\)
Để hàm số này đồng biến trên R thì \(\dfrac{2m-1}{-5m-10}>0\)
=>\(\dfrac{2m-1}{m+2}< 0\)
TH1: \(\left\{{}\begin{matrix}2m-1>0\\m+2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{1}{2}\\m< -2\end{matrix}\right.\)
=>\(m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}2m-1< 0\\m+2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< \dfrac{1}{2}\\m>-2\end{matrix}\right.\)
=>\(-2< m< \dfrac{1}{2}\)
Vậy: \(-2< m< \dfrac{1}{2}\)
Đúng 0
Bình luận (0)
làm hết giú tui nhanh

Bài `1`
\(a,35-\left\{12-\left[\left(-14\right)+\left(-2\right)\right]\right\}\\ =35-\left[12-\left(-16\right)\right]\\ =35-\left(12+16\right)\\ =35-28\\ =7\\ b,1997-\left[10\cdot\left(4^3-56\right):2^3+2^3\right]\cdot2023^0\\ =1997-\left[10\cdot\left(64-56\right):8+8\right]\cdot1\\ =1997-\left(10\cdot8:8+8\right)\\ =1997-\left(80:8+8\right)\\ =1997-\left(10+8\right)\\ =1997-18\\ =1979\)
Bài `2`
`124+(118-x)=217`
`=>118-x=217-124`
`=>118-x=93`
`=>x=118-93`
`=>x=25`
`3^(x+2)+3^x=10`
`=>3^x(3^2 +1)=10`
`=> 3^x*10=10`
`=>3^x=1`
`=> x=0`
Đúng 1
Bình luận (0)
Bài 5:
\(B=3+3^2+3^3+...+3^{2015}\)
=>\(3B=3^2+3^3+...+3^{2016}\)
=>\(3B-B=3^2+3^3+...+3^{2016}-3-3^2-...-3^{2015}\)
=>\(2B=3^{2016}-3\)
=>\(2B+3=3^{2016}\) là lũy thừa của 3(ĐPCM)
Bài 3:
\(96=2^5\cdot3;120=2^3\cdot3\cdot5;72=2^3\cdot3\)
=>\(ƯCLN\left(96;120;72\right)=2^3\cdot3=24\)
Để phân chia 96 bạn thi Văn, 120 bạn thi Toán và 72 bạn thi Anh ra thành các hàng sao cho mỗi hàng có số bạn thi mỗi môn bằng nhau thì số hàng và số bạn mỗi hàng phải là ước chung của 96;120;72
=>Để số hàng ít nhất số học sinh mỗi hàng là lớn nhất
=>Số hàng ít nhất khi số học sinh mỗi hàng là ƯCLN(72;96;120)=24 bạn/hàng
Số hàng khi đó là:
\(\dfrac{72+96+120}{24}=3+4+5=12\left(hàng\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giú vs ạ mình cám ơn

Gọi độ dài quãng đường AB là x
Theo đề, ta có phương trình:
\(\dfrac{1}{50}x+\dfrac{1}{40}x=\dfrac{5}{2}-\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{9}{200}x=\dfrac{9}{4}\)
hay x=50
Đúng 1
Bình luận (1)


























