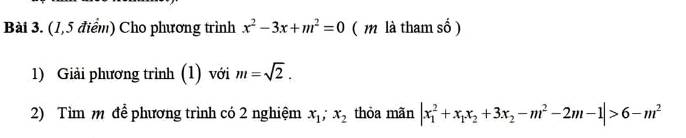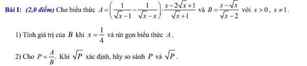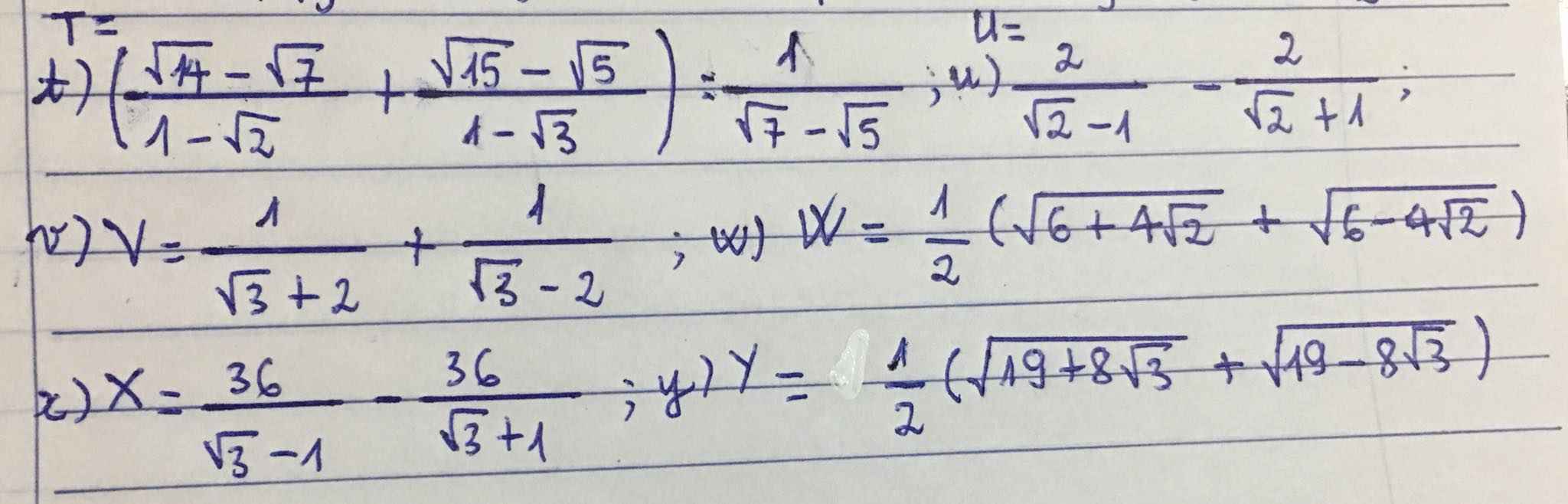Lời giải:
Theo định lý Viet:
$x_1+x_2=3$
$x_1x_2=m^2$
Khi đó:
$|x_1^2+x_1x_2+3x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+x_1x_2+(x_1+x_2)x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+2x_1x_2+x_2^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |(x_1+x_2)^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |9-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |m^2+2m-8|> 6-m^2$
Nếu $m^2+2m-8\geq 0$ thì:
$m^2+2m-8> 6-m^2$
$\Leftrightarrow 2m^2+2m-14>0$
$\Leftrightarrow m^2+m-7>0$
$\Leftrightarrow m< \frac{-1-\sqrt{29}}{2}$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Kết hợp với $m^2+2m-8\geq 0$ suy ra $m\leq -4$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Nếu $m^2+2m-8<0$ thì:
$-(m^2+2m-8)> 6-m^2$
$\Leftrightarrow m< 1$
Kết hợp với $m^2+2m-8<0$ suy ra $-4< m< 1$
Vậy........