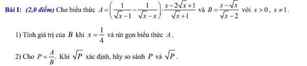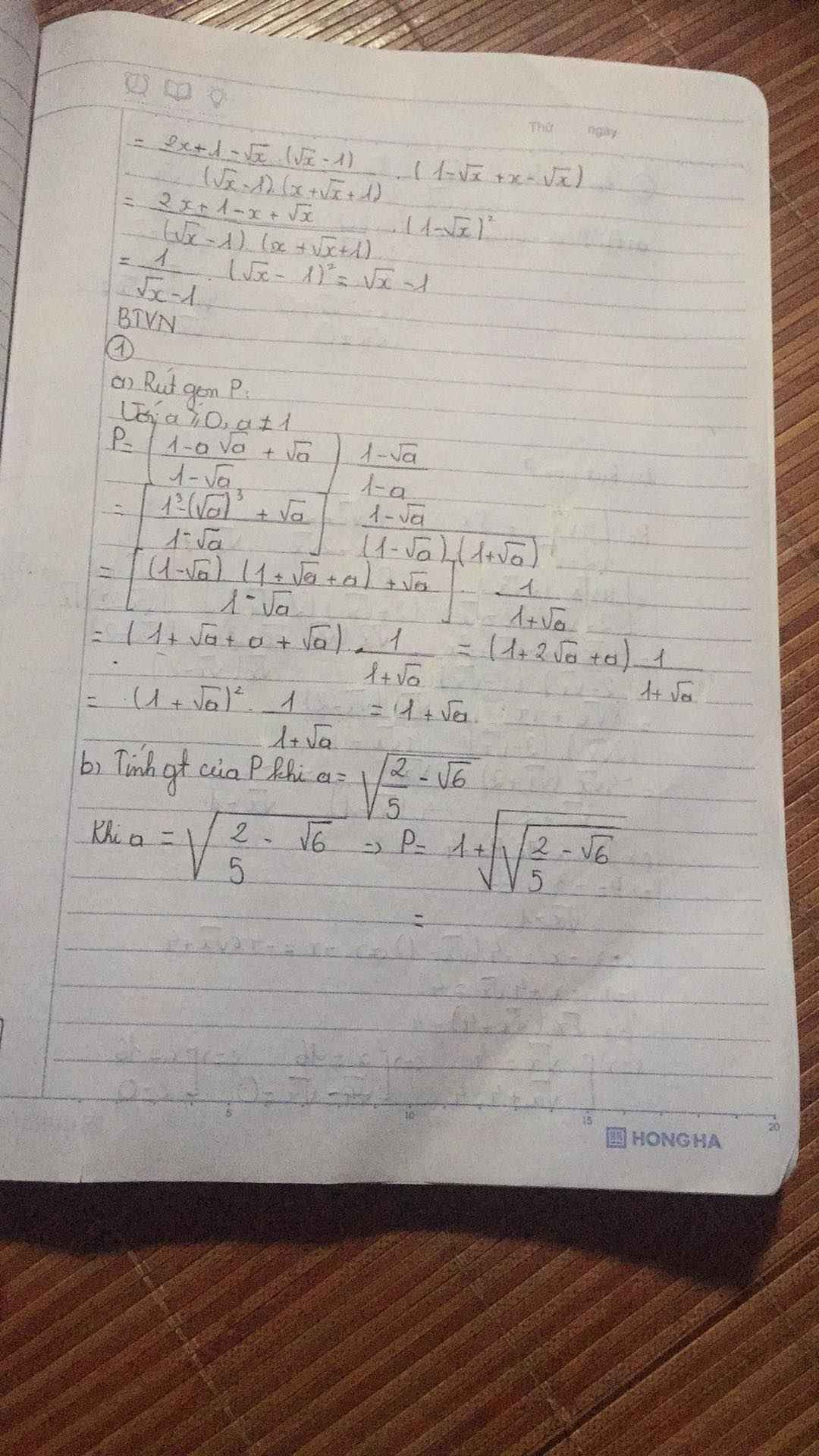1: Thay x=1/4 vào B, ta được:
\(B=\dfrac{\dfrac{1}{4}-\dfrac{1}{2}}{\dfrac{1}{2}-2}=\dfrac{1}{6}\)
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
2: \(P=A:B=\dfrac{\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}-2}{x}\)
Để \(\sqrt{P}\) xác định thì x>4
\(P^2-P=\dfrac{x-4\sqrt{x}+4}{x^2}-\dfrac{\sqrt{x}-2}{x}\)
\(=\dfrac{x-4\sqrt{x}+4-x\sqrt{x}+2\sqrt{x}}{x^2}=\dfrac{x-x\sqrt{x}-2\sqrt{x}+4}{x^2}>0\)
=>\(P^2>P\)
hay \(P>\sqrt{P}\)