cho tam giác ABC vuông tại đỉnh A, A(-1;4), B(1;-4) và đường thẳng BC đi qua điểm M\(\left(2;\dfrac{1}{2}\right)\). xác định tọa độ đỉnh C

Những câu hỏi liên quan
Câu 1. Tam giác ABC cân tại B có0 B 40 thì A bằng:A) 400 B) 700 C) 600 D) 500Câu 2. Tam giác AED có AD2 DE2 - AE2thì tam giác AEDA) vuông tại E B) vuông tại D C) vuông tại A D) không vuôngCâu 3. Cho tam giác ABC và tam giác có ba đỉnh D; E; F, biết AB EF, B F . Cần thêm điềukiện gì để hai tam giác bằng nhau theo trường hợp: góc - cạnh - góc?A) AC FD B) A F C) CE D) AECâu 4. Cho tam giác DEF vuông cân tại D, có DE3cm thì EF bằng:A) 18cm B) 12cm C) 12 cm D) 18 cmII. BÀI TẬP TỰ LUẬN (8 điể...
Đọc tiếp
Câu 1. Tam giác ABC cân tại B có
0 B 40 thì A bằng:
A) 400 B) 70
0 C) 60
0 D) 50
0
Câu 2. Tam giác AED có AD2 = DE2 - AE2thì tam giác AEDA) vuông tại E B) vuông tại D C) vuông tại A D) không vuôngCâu 3. Cho tam giác ABC và tam giác có ba đỉnh D; E; F, biết AB = EF, B =F . Cần thêm điềukiện gì để hai tam giác bằng nhau theo trường hợp: góc - cạnh - góc?A) AC = FD B) A =F C) C=E D) A=ECâu 4. Cho tam giác DEF vuông cân tại D, có DE=3cm thì EF bằng:A) 18cm B) 12cm C) 12 cm D) 18 cm
II. BÀI TẬP TỰ LUẬN (8 điểm)Cho tam giác ABC có
0 A 90 và AB < BC. Gọi M là trung điểm của AC, trên tia đối của tia MB
lấy điểm D sao cho MD = MB. 1) Chứng minh ABM = CDM từ đó chứng minh AB=CD và AB //
Câu 1: B
Câu 2:Sửa đề: \(AD^2=DE^2+AE^2\)
=> Chọn A
Câu 3: Chọn D
Câu 4: \(EF=3\sqrt{2}cm\)
Đúng 1
Bình luận (0)
cho tam giác vuông ABC vuông tại A. Phân giác tại đỉnh B cắt phân giác tại đỉnh C tại D.
CMr BE.CF=2BD.DC
cho tam giác ABC vuông tại A biết B^ = 70° tính được góc ngoài của tam giác ABC tại đỉnh C là
có : ( tổng ba góc của một tam giác )
Mà ( hai góc kề bù )
Đúng 0
Bình luận (0)
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a) Tam giác ABC nhọn:
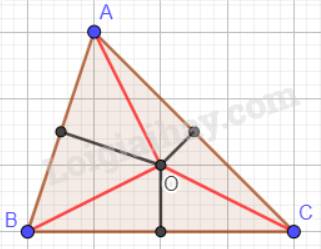
b) Tam giác ABC vuông tại A:
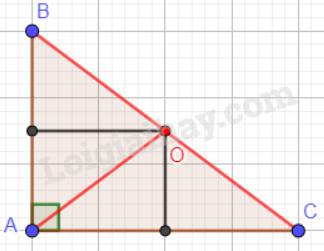
c) Tam giác ABC có góc A tù:
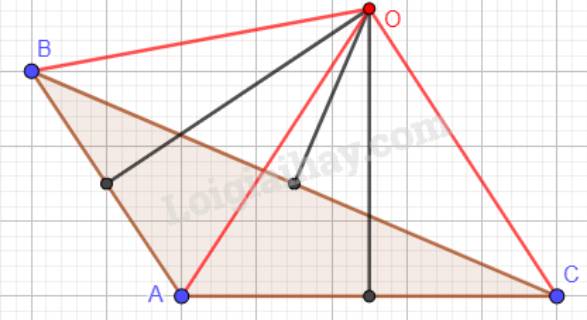
Đúng 0
Bình luận (0)
cho tam gaics ABC vuông góc tại đỉnh C. Về phía ngoài tam giác, ta dựng các tam giác ABD vuông cân tại đỉnh D, tam giác ACE vuông cân ở M: a)CM tứ giác BAMD là hình thang vuông b)CM hệ thức DM=BD+CM
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
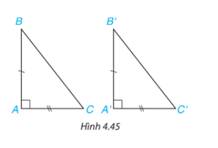
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông góc tại A. Góc ngoài tại đỉnh B là góc?
Xem chi tiết
\(\Delta ABC\perp A\) \(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
= > Góc B và Góc C phải là 2 góc nhọn
Góc ngoài đỉnh B = \(180^0-\widehat{B}\)mà Góc B nhọn = > Góc ngoài tại đỉnh B là góc tù
Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi AE là tia phân giác
góc ngoài của tam giác ABC tại đỉnh A, nó cắt BC ở E. Chứng minh: \(\dfrac{1}{AB^2}\) +\(\dfrac{1}{AC^2}\)= \(\dfrac{1}{AD^2}+\dfrac{1}{AE^2}\)
Kẻ \(AH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông BAC có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
Do AD và AE lần lượt là hai tia phân giác trong và ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\)
Áp dụng hệ thức lượng vào tam giác vuông AED có:
\(\dfrac{1}{AE^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}\) (AH là đường cao của tam giác AED do \(AH\perp BC\) hay \(AH\perp ED\))
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AE^2}+\dfrac{1}{DA^2}\)
Vậy...
Đúng 5
Bình luận (0)
Cho Tam giác abc vuông tại a gọi h là chân đường vuông góc kẻ từ a Đến cạnh bc. Tìm khoảng cách từ đỉnh a b c Đến các cạnh của tam giác abc
h(A;BC)=AH
h(B;AC)=BA
h(C;AB)=CA
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại đỉnh A có AB = AC. Điểm I nằm trong tam giác ABC sao cho MA : MB : MC = 1 : 2 : 3. Tính số đo góc AIC






















