Viết phương trình đường tròn biết: đường kính AB với A(3;3) và B(1;5)

Những câu hỏi liên quan
viết phương trình đường tròn đường kính ab. biết a(4;-1) ,b(1;-4)
Tọa độ tâm I là:
x=(4+1)/2=5/2 và y=(-1-4)/2=-5/2
=>I(2,5;-2,5)
\(IA=\sqrt{\left(2,5-4\right)^2+\left(-2,5+1\right)^2}=\dfrac{3\sqrt{2}}{2}\)
Phương trình (C) là:
(x-2,5)^2+(y+2,5)^2=9/2
Đúng 2
Bình luận (0)
Viết phương trình đường tròn đường kính AB với A(-1;-2), B(-3;0)
Tọa độ tâm I là:
\(\left\{{}\begin{matrix}x_I=\dfrac{-1-3}{2}=-2\\y_I=\dfrac{-2+0}{2}=-1\end{matrix}\right.\)
\(R=AI=\sqrt{\left(-2+1\right)^2+\left(-1+2\right)^2}=\sqrt{2}\)
Phương trình đường tròn là:
\(\left(x+2\right)^2+\left(y+1\right)^2=2\)
Đúng 3
Bình luận (0)
Câu 12: Trong mặt phẳng tọa độ, cho A(-1;-3),B(-3;5). a. Viết phương trình tham số của đường thẳng AB. b. Viết phương trình đường tròn đường kính AB.
\(AB\left\{{}\begin{matrix}quaA\left(-1;-3\right)\\VTCP\overrightarrow{AB}=\left(-2;8\right)\end{matrix}\right.\)
\(PTTS\) của \(AB:\left\{{}\begin{matrix}x=-1-2t\\y=-3+8t\end{matrix}\right.\)
Gọi \(I\left(x_I;y_I\right)\) là tâm đường tròn
\(I\) là trung điểm \(AB\)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1-3}{2}=-2\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-3+5}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(-2;1\right)\)
\(AB=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)
Mà \(R=\dfrac{AB}{2}=\dfrac{2\sqrt{17}}{2}=\sqrt{17}\)
Vậy \(PT\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=17\)
Đúng 3
Bình luận (1)
Cho △ABC biết A(-2;4) B(5;5) C(6;-2)
a) Viết phương trình đường thẳng đi qua C và vuông góc với AB
b) Viết phương trình đường trung tuyến BK
c) Viết phương trình đường tròn tâm B,bán kính AC
d) Viết phương trình đi qua 3 điểm A,B,C
a: vecto AB=(7;1)
=>(d) có VTPT là (7;1)
Phương trình (d) là;
7(x-6)+1(y+2)=0
=>7x+y-40=0
b: Tọa độ K là:
x=(6-2)/2=2 và y=(4-2)/2=1
B(5;5); K(2;1)
vecto BK=(-3;-4)=(3;4)
=>VTPT là (-4;3)
Phương trình BK là:
-4(x-2)+3(y-1)=0
=>-4x+8+3y-3=0
=>-4x+3y+5=0
c: \(AC=\sqrt{\left(6+2\right)^2+\left(-2-4\right)^2}=10\)
Phương trình (C) là:
(x-5)^2+(y-5)^2=10^2=100
Đúng 1
Bình luận (0)
Cho A (-3;-2) B (1;-4)
a) Viết phương trình tham số của đường thẳng AB
b) Viết phương trình đường tròn tâm A bán kính AB
a: vecto AB=(4;-2)
=>Phương trình tham số là:
\(\left\{{}\begin{matrix}x=-3+4t\\y=-2-2t\end{matrix}\right.\)
b: \(AB=\sqrt{\left(1+3\right)^2+\left(-4+2\right)^2}=\sqrt{4^2+2^2}=2\sqrt{5}\)
Phương trình đường tròn tâm A bán kính AB là:
(x+3)^2+(y+2)^2=20
Đúng 2
Bình luận (0)
Cho A(1;2) , B(5;2) a), Viết phương trình đường tròn nhận AB làm đường kính. b), viết phương trình đường tròn tâm A và đi qua B.
\(\overrightarrow{AB}=\left(4;0\right)\Rightarrow AB=4\)
Gọi I là trung điểm AB \(\Rightarrow I\left(3;2\right)\)
Đường tròn đường kính AB nhận I là trung điểm và có bán kính \(R=\dfrac{AB}{2}=2\)
Phương trình: \(\left(x-3\right)^2+\left(y-2\right)^2=4\)
b.
\(R=AB=4\)
Phương trình: \(\left(x-1\right)^2+\left(y-2\right)^2=16\)
Đúng 0
Bình luận (0)
a, Tâm I của đường tròn: \(I=\left(\dfrac{1+5}{2};\dfrac{2+2}{2}\right)=\left(3;2\right)\)
Bán kính: \(R=\dfrac{AB}{2}=\dfrac{\sqrt{\left(5-1\right)^2+\left(2-2\right)^2}}{2}=2\)
Phương trình đường tròn: \(\left(x-3\right)^2+\left(y-2\right)^2=4\)
b, Tâm I của đường tròn: \(I\equiv A=\left(1;2\right)\)
Bán kính: \(R=AB=\sqrt{\left(5-1\right)^2+\left(2-2\right)^2}=4\)
Phương trình đường tròn: \(\left(x-1\right)^2+\left(y-2\right)^2=16\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(1;2), B(3;-1), C(-2;1)
a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
b) Viết phương trình đường tròn đường kính AB
a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
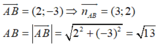
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
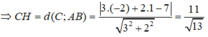
Diện tích tam giác ABC là:
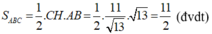
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
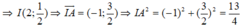
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
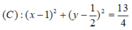
Đúng 0
Bình luận (0)
Viết phương trình đường tròn (C) trong trường hợp sau
(C) có đường kính AB với A(1;1), B(7;5)
Tọa độ tâm là:
\(\left\{{}\begin{matrix}x_O=\dfrac{1+7}{2}=4\\y_O=\dfrac{1+5}{2}=3\end{matrix}\right.\)
Vậy: Tọa độ tâm là O(4;3)
\(OA=\sqrt{\left(4-1\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
Phương trình đường tròn là:
\(\left(x-4\right)^2+\left(y-3\right)^2=13\)
Đúng 1
Bình luận (0)
Cho hai điểm A(3; -4) và B(-3; 4).
Viết phương trình đường tròn (C) nhận AB là đường kính.
Gọi I là tâm đường tròn nhận AB là đường kính
⇒ I là trung điểm của AB ⇒ I (0; 0)
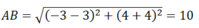
⇒ R = AB/2 = 5
Phương trình đường tròn (C) nhận AB là đường kính là:
x2 + y2 = 25
Đúng 0
Bình luận (0)


















![[柠檬]๛Čɦαŋɦ ČŠツ](https://hoc24.vn/images/avt/avt6342624_256by256.jpg)