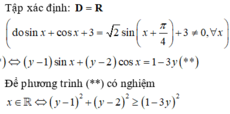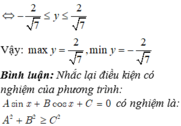Tìm GTLN của hàm số y=-(x-3)(x+3)

Những câu hỏi liên quan
24. Tìm GTLN của hàm số: \(y=3\cos\left(x-\dfrac{\pi}{2}\right)+1\)
26. a) Tìm GTLN của hàm số: \(y=\cos2x+\sin2x\)
b) Giải PT: \(\sin x+\sqrt{3}\cos x=1\)
24.
\(cos\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
\(y_{max}=4\)
26.
\(y=\sqrt{2}cos\left(2x-\dfrac{\pi}{4}\right)\)
Do \(cos\left(2x-\dfrac{\pi}{4}\right)\le1\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\)
b.
\(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 4
Bình luận (0)
TÌM GTNN CỦA HÀM SỐ SAU:
a) y=\(\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}\)
TÌM GTLN CỦA HÀM SỐ SAU:
b)y= \(x^2\sqrt{9-x^2}với-3\le x\le3\)
c)y=\(\left(1-x\right)^3\left(1+3x\right)với\dfrac{-1}{3}\le x\le1\)
\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Tìm GTLN và GTNN của hàm số
y
sin
x
+
2
cos
x
+
1
sin
x
+
cos
x
+
3
(*) A.
m
a
x
y
4...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
A. m a x y = 4 7 , m i n y = - 4 7
B. m a x y = 2 7 7 , m i n y = - 2 7 7
C. m a x y = 7 2 , m i n y = - 2 7
D. m a x y = 2 7 7 , m i n y = - 2 7 7
Tìm gtln gtnn của hàm số y= cos^2 x - 4sin4x +3
Tìm GTLN ,GTNN của hàm số sau :
\(y=\sqrt{3+x}+\sqrt{5-x}\)
Help me
Ta có: \(y=\sqrt{3+x}+\sqrt{5-x}\)
ĐKXĐ: \(-3\le x\le5\)
\(y^2=3+x+5-x+2\sqrt{\left(3+x\right)\left(5-x\right)}=8+2\sqrt{\left(3+x\right)\left(5-x\right)}\)\(\ge8\)
\(\Rightarrow y\ge2\sqrt{2}\)
Dấu "=" xảy ra khi và chỉ khi \(\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)(thỏa mãn)
Vậy min y = \(2\sqrt{2}\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)
mặt khác \(y^2\) = \(8+2\sqrt{\left(3+x\right)\left(5-x\right)}\le8+3+x+5-x=16\)
\(\Rightarrow y\le4\)
Dấu"=" xảy ra khi và chỉ khi \(3+x=5-x\Leftrightarrow x=1\)(thỏa mãn)
Vậy max y = 4 \(\Leftrightarrow x=1\)
Đúng 1
Bình luận (0)
Tìm GTLN của hàm số \(y=\left(x+2\right)\left(3-x\right)\), với \(-2\le x\le3\).
\(y=\left(x+2\right)\left(3-x\right)\)
\(=3x-x^2+6-2x\)
\(=-x^2+x+6\)
=>y'=-2x+1
Đặt y'=0
=>-2x+1=0
=>-2x=-1
=>\(x=\dfrac{1}{2}\)
\(f\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}+2\right)\left(3-\dfrac{1}{2}\right)=\dfrac{5}{2}\cdot\dfrac{5}{2}=\dfrac{25}{4}\)
\(f\left(-2\right)=\left(-2+2\right)\left(3+2\right)=0\)
\(f\left(3\right)=\left(3+2\right)\left(3-3\right)=0\)
=>\(y_{max\left[-2;3\right]}=\dfrac{25}{4}\)
Đúng 0
Bình luận (0)
1/ Xét tính chẵn lẻ của hàm số: y = f(x) = căn (2-sin3x) - căn(2+sin3x) 2/ Tìm GTLN-GTNN của hàm số sau: y = f(x)= cos2x + 3 sin2sin2x - 2
Tìm GTLN/GTNN của hàm số: \(y=sin^4\left(x+\dfrac{\pi}{3}\right)+2\)
`TXĐ: R`
Ta có: `-1 <= sin(x+ \pi/3) <= 1`
`<=>0 <= sin^4 (x+\pi/3) <= 1`
`<=>2 <= y <= 3`
`=>y_[mi n]=2<=>sin(x +\pi/3)=0<=>x= -\pi/3+k\pi` `(k in ZZ)`
`y_[max]=3<=>sin(x +\pi/3)=1<=>x=\pi/6 +k2\pi` `(k in ZZ)`
Đúng 2
Bình luận (2)
hộ cái nha:
Cho hàm số y=x^2−4x+3.Tìm GTLN,GTNN của hàm số trên đoạn [0;3].