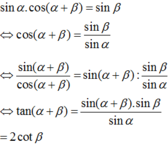Tìm lim un với un=\(\sum\limits^n_{k=1}sin^k\alpha\) (α≠\(\dfrac{\pi}{2}\) +kπ, k ϵ Z)

Những câu hỏi liên quan
\(Un=\dfrac{4n}{12+\left(2+n^2\right)^2}\)
\(An=\sum\limits^n_{k=1}Uk\) , Tính lim An
Em cảm ơn ạ !!!!
\(u_n=\dfrac{4n}{n^4+4n^2+16}=\dfrac{4n}{n^4+8n^2+16-4n^2}=\dfrac{4n}{\left(n^2+4\right)^2-4n^2}=\dfrac{4n}{\left(n^2-2n+4\right)\left(n^2+2n+4\right)}\)
\(=\dfrac{1}{n^2-2n+4}-\dfrac{1}{n^2+2n+4}=\dfrac{1}{\left(n-1\right)^2+3}-\dfrac{1}{\left(n+1\right)^2+3}\)
Do đó:
\(A_n=\dfrac{1}{\left(1-1\right)^2+3}-\dfrac{1}{\left(1+1\right)^2+3}+\dfrac{1}{\left(2-1\right)^2+3}-\dfrac{1}{\left(2+1\right)^2+3}+...+\dfrac{1}{\left(n-1\right)^2+3}-\dfrac{1}{\left(n+1\right)^2+3}\)
\(=\dfrac{1}{0^2+3}-\dfrac{1}{2^2+3}+\dfrac{1}{1^2+3}-\dfrac{1}{3^2+3}+\dfrac{1}{2^2+3}-\dfrac{1}{4^2+3}+...+\dfrac{1}{\left(n-1\right)^2+3}-\dfrac{1}{\left(n+1\right)^2+3}\)
\(=\dfrac{1}{0^2+3}+\dfrac{1}{1^2+3}-\dfrac{1}{n^2+3}-\dfrac{1}{\left(n+1\right)^2+3}=\dfrac{7}{12}-\dfrac{1}{n^2+3}-\dfrac{1}{\left(n+1\right)^2+3}\)
\(\Rightarrow\lim\left(A_n\right)=\dfrac{7}{12}\)
Đúng 0
Bình luận (0)
Cho dãy (Un) thỏa: \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{u_n^{2015}+u_n+1}{u_n^{2014}-u_n+3}\end{matrix}\right.\).
a) CMR: \(u_n>1\) với mọi N và Un là dãy tăng
b) Tính: \(lim\sum\limits^n_{i=1}\dfrac{1}{u_i^{2014}+2}\)
Cho dãy (Un) thỏa: \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{u_n^{2015}+u_n+1}{u_n^{2014}-u_n+3}\end{matrix}\right.\).
a) CMR: \(u_n>1\) với mọi N và Un là dãy tăng
b) Tính: \(lim\sum\limits^n_{i=1}\dfrac{1}{u_i^{2014}+2}\)
a) Để chứng minh rằng Un > 1 đối với mọi N và Un là dãy tăng, ta có thể sử dụng phương pháp quy nạp.
Bước cơ sở: Ta thấy rằng u1 = 2 > 1.
Bước giả sử: Giả sử đúng đối với một số nguyên k ≥ 1, tức là uk > 1.
Bước bước: Ta sẽ chứng minh rằng uk+1 > 1. Từ công thức cho dãy (Un), ta có:
uk+1 = uk-2015 + uk + 1/uk - uk + 3
Vì uk > 1 (theo giả thiết giả sử), ta có uk - 2015 > 0 và uk + 3 > 0. Do đó, uk+1 > 0.
Vì vậy, ta có uk+1 > 1, và đẳng thức này đúng đối với mọi số nguyên k ≥ 1.
Do đó, ta chứng minh được rằng Un > 1 đối với mọi N và Un là dãy tăng.
b) Để tính limn∑i=11uk - i + 2, ta có thể sử dụng định nghĩa của dãy (Un) và công thức tổng của dãy số aritmeti.
Từ công thức cho dãy (Un), ta có:
uk - i + 2 = uk - 2015 - i + uk + 1 - i + uk + 2 - i
Vì Un là dãy tăng, ta có thể viết lại công thức trên như sau:
uk - i + 2 = uk - 2015 - i + uk + 1 - i + uk + 2 - i
= (uk+1 - 2015 + uk + 1) - (uk - 2015 + uk) + (uk+1 - uk)
= 2uk+1 - 2uk + 2015
Do đó, ta có thể viết lại tổng như sau:
∑i=11uk - i + 2 = 2∑i=11uk+1 - 2∑i=11uk + 2015∑i=1
= 2(u12 - u2) + 2015(12)
Với giá trị cụ thể của u12 và u2, ta có thể tính được tổng trên.
Đúng 1
Bình luận (0)
Rút gọn :
a, \(A=\sum\limits^n_{k=1}k.k!\)
b, \(B=\sum\limits^n_{k=2}\dfrac{k}{\left(k-1\right)!}\)
Tính \(lim\dfrac{\prod\limits^n_{k=1}\left(2k-1\right)}{\prod\limits^n_{k=1}\left(2k\right)}\)
Bạn tham khảo cách làm nha
https://diendantoanhoc.org/topic/106253-lim-nto-inftyprod-k1nfrac2k-12k/
Đúng 2
Bình luận (0)
\(\left(x_n\right)\left\{{}\begin{matrix}x_1=2\\x_{n+1}=\dfrac{x_n+2+\sqrt{x_n^2+8x_n-4}}{2},n\in N,n>0\end{matrix}\right.\)
Đặt \(y_n=\sum\limits^n_{k=1}\dfrac{1}{x_n^2-4}\). Tìm lim yn
Chứng minh:
a)
\(\sum\limits^n_{i=1}cos\dfrac{2\left(i-1\right)\pi}{n}=0\)
b) \(\sum\limits^n_{i=1}sin\dfrac{2\left(i-1\right)\pi}{n}=0\)
Chứng minh rằng: \(\sum\limits^n_{k=1}\dfrac{k}{k^4+5k^2+6}< \dfrac{1}{2}\)
Mình cần gấp ạ
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα