B7:

Diện tích mảnh đất:

30 x 20 = 600(m²)

Bán kính ao:

15:2=7,5(m)

Diện tích ao:

7,5 x 7,5 x 3,14=176,625(m²)

Diện tích phần đất còn lại:

600 - 176,625 = 423,375 (m²)

Đ.số: 423,375m²

Bài 6 :

Vận tốc khi lên đèo :

\(v=\dfrac{s}{t}=\dfrac{45}{2,5}=18\left(\dfrac{km}{h}\right)\)

Vận tốc khi xuống đèo :

\(v=\dfrac{s}{t}=\dfrac{30}{0,5}=60\left(\dfrac{km}{h}\right)\)

Vận tốc tb : 

\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{45+30}{2,5+0,5}=25\left(\dfrac{km}{h}\right)\)

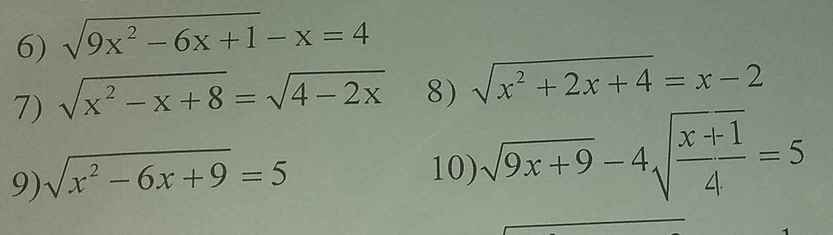
7)Đk \(x\le2\)

Pt \(\Leftrightarrow x^2-x+8=4-2x\)

\(\Leftrightarrow x^2+x+4=0\)

\(\Delta=-15< 0\) => vô nghiệm

Vậy pt vô nghiệm

10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)

\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)

\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)

\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)

Vậy \(S=\left\{24\right\}\)

Jane and Lan are going to invite lots of people.

Jane and Lan intend to invite lots of people

A nhá bạn 

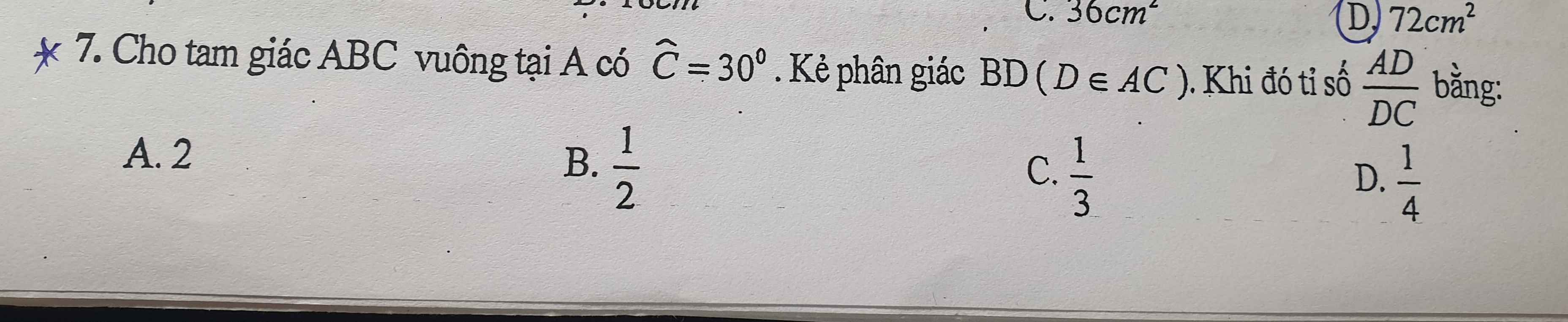
đầu tiên bạn áp dụng tc cạnh đối diện với góc 30 độ trong tg vuông có

AB=\(\dfrac{1}{2}\)BC\(\Rightarrow\dfrac{BC}{AB}=2\)

Áp dụng tc đường phân giác có

\(\dfrac{CD}{DA}=\dfrac{CB}{AB}=2\)

OK chưa bạn cho mình 1 tick nhá

Câu 1: 

a: \(=2x^4-6x^2\)

b: \(=3y^2+2\)

Câu 1:

\(a,=2x^4-6x^2\\ b,=3y^2+2\)

Câu 2:

\(\widehat{C}=360^0-55^0-80^0-120^0=105^0\\ \Rightarrow\text{Góc ngoài tại }\widehat{C}=180^0-105^0=75^0\)

Câu 3:

\(a,AM=\dfrac{BC}{2}=\dfrac{\sqrt{AB^2+AC^2}}{2}=\dfrac{15}{2}\left(cm\right)\\ b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot12\cdot9=54\left(cm^2\right)\)

Câu 4:

\(a,=\dfrac{x^2-4x+4}{x-2}=\dfrac{\left(x-2\right)^2}{x-2}=x-2\\ b,=\dfrac{x+1+2x+3-4+x}{6x^2y}=\dfrac{4x}{6x^2y}=\dfrac{2}{3xy}\)

Câu 5:

\(a,=6x\left(y-2x\right)\\ b,=x^2\left(x+y\right)-\left(x+y\right)=\left(x-1\right)\left(x+1\right)\left(x+y\right)\\ c,=3x^2-3x-4x+4=\left(x-1\right)\left(3x-4\right)\)

Câu 6:

Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC

Do đó \(MN=\dfrac{1}{2}BC=5\left(cm\right)\)

Câu 8:

\(a,=\dfrac{5\left(x+y\right)}{\left(x+y\right)^2}=\dfrac{5}{x+y}\\ b,\Rightarrow x\left(x-5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

Ta có:

\(cos20^0=sin70^0\)

\(cos55^0=sin35^0\)

\(\)Lại có:\(sin\alpha< tan\alpha\)

=> \(sin35^0< sin38^0< sin70^0< sin88^0< tan48^0\)

=> \(cos55^0< sin38^0< cos20^0< sin88^0< tan48^0\)

1: Xét ΔDEF vuông tại D có DK là đường cao

nên \(EK\cdot EF=DE^2;FK\cdot FE=DF^2\)

=>\(\frac{DE^2}{DF^2}=\frac{EK\cdot EF}{FK\cdot EF}=\frac{EK}{FK}\)

2: Xét ΔDKE vuông tại K có KA là đường cao

nên \(DA\cdot DE=DK^2\left(1\right)\)

Xét ΔDEF vuông tại D có DK là đường cao

nên \(KE\cdot KF=DK^2\left(2\right)\)

Từ (1),(2) suy ra \(DA\cdot DE=KE\cdot KF\)

3: Xét ΔDKF vuông tại K có KB là đường cao

nên \(DB\cdot DF=DK^2\) (3)

Từ (1),(3) suy ra \(DA\cdot DE=DB\cdot DF\)

4: Xét tứ giác DAKB có \(\hat{DAK}=\hat{DBK}=\hat{BDA}=90^0\)

nên DAKB là hình chữ nhật

=>DK=AB

\(EK^3+FK^3+3\cdot AB\cdot DE\cdot DF\)

\(=EK^3+FK^3+3\cdot DK\cdot\frac{DK^2}{DA}\cdot\frac{DK^2}{DB}\)

\(=EK^3+FK^3+3\cdot DK^2\cdot\frac{DK}{DA}\cdot\frac{DK^2}{DB}\)

\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\frac{DK^3}{DA\cdot DB}\)

\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\frac{DK^3}{\frac{DK^2}{DE}\cdot\frac{DK^2}{DF}}\)

\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot DK^3\cdot\frac{DE\cdot DF}{DK^4}\)

\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\frac{DE\cdot DF}{DK}\)

\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot EF\)

\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\left(EK+FK\right)=\left(EK+FK\right)^3=EF^3\)

5: \(KB\cdot DE+KA\cdot DF\)

\(=DA\cdot DE+DB\cdot DF=DK^2+DK^2=2DK^2\)

\(=2\cdot KE\cdot KF\)

6:

Xét ΔDKE vuông tại K có KA là đường cao

nên \(AD\cdot AE=AK^2\)

Xét ΔDKF vuông tại K có KB là đường cao

nên \(BD\cdot BF=BK^2\)

\(AD\cdot AE+BD\cdot BF\)

\(=AK^2+KB^2=KD^2\)

\(=KE\cdot KF\)

7: Xét ΔDKE vuông tại K có KA là đường cao

nên \(EA\cdot ED=EK^2\)

=>\(EA=\frac{EK^2}{ED}\)

Xét ΔDKF vuông tại K có KB là đường cao

nên \(FB\cdot FD=FK^2\)

=>\(FB=\frac{FK^2}{FD}\)

\(EF\cdot AE\cdot BF=EF\cdot\frac{EK^2}{ED}\cdot\frac{KF^2}{FD}=\frac{EF}{ED\cdot FD}\cdot EK^2\cdot KF^2\)

\(=\frac{EF}{DK\cdot EF}\cdot\left(EK\cdot KF\right)^2=\frac{1}{DK}\cdot DK^4=DK^3\)

\(=AB^3\)