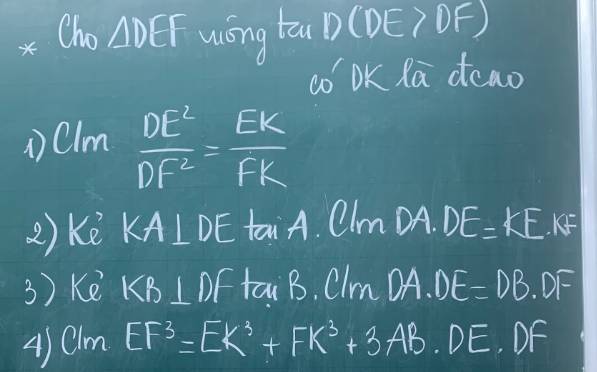1: Xét ΔDEF vuông tại D có DK là đường cao
nên \(EK\cdot EF=DE^2;FK\cdot FE=DF^2\)
=>\(\frac{DE^2}{DF^2}=\frac{EK\cdot EF}{FK\cdot EF}=\frac{EK}{FK}\)
2: Xét ΔDKE vuông tại K có KA là đường cao
nên \(DA\cdot DE=DK^2\left(1\right)\)
Xét ΔDEF vuông tại D có DK là đường cao
nên \(KE\cdot KF=DK^2\left(2\right)\)
Từ (1),(2) suy ra \(DA\cdot DE=KE\cdot KF\)
3: Xét ΔDKF vuông tại K có KB là đường cao
nên \(DB\cdot DF=DK^2\) (3)
Từ (1),(3) suy ra \(DA\cdot DE=DB\cdot DF\)
4: Xét tứ giác DAKB có \(\hat{DAK}=\hat{DBK}=\hat{BDA}=90^0\)
nên DAKB là hình chữ nhật
=>DK=AB
\(EK^3+FK^3+3\cdot AB\cdot DE\cdot DF\)
\(=EK^3+FK^3+3\cdot DK\cdot\frac{DK^2}{DA}\cdot\frac{DK^2}{DB}\)
\(=EK^3+FK^3+3\cdot DK^2\cdot\frac{DK}{DA}\cdot\frac{DK^2}{DB}\)
\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\frac{DK^3}{DA\cdot DB}\)
\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\frac{DK^3}{\frac{DK^2}{DE}\cdot\frac{DK^2}{DF}}\)
\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot DK^3\cdot\frac{DE\cdot DF}{DK^4}\)
\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\frac{DE\cdot DF}{DK}\)
\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot EF\)
\(=EK^3+FK^3+3\cdot EK\cdot FK\cdot\left(EK+FK\right)=\left(EK+FK\right)^3=EF^3\)
5: \(KB\cdot DE+KA\cdot DF\)
\(=DA\cdot DE+DB\cdot DF=DK^2+DK^2=2DK^2\)
\(=2\cdot KE\cdot KF\)
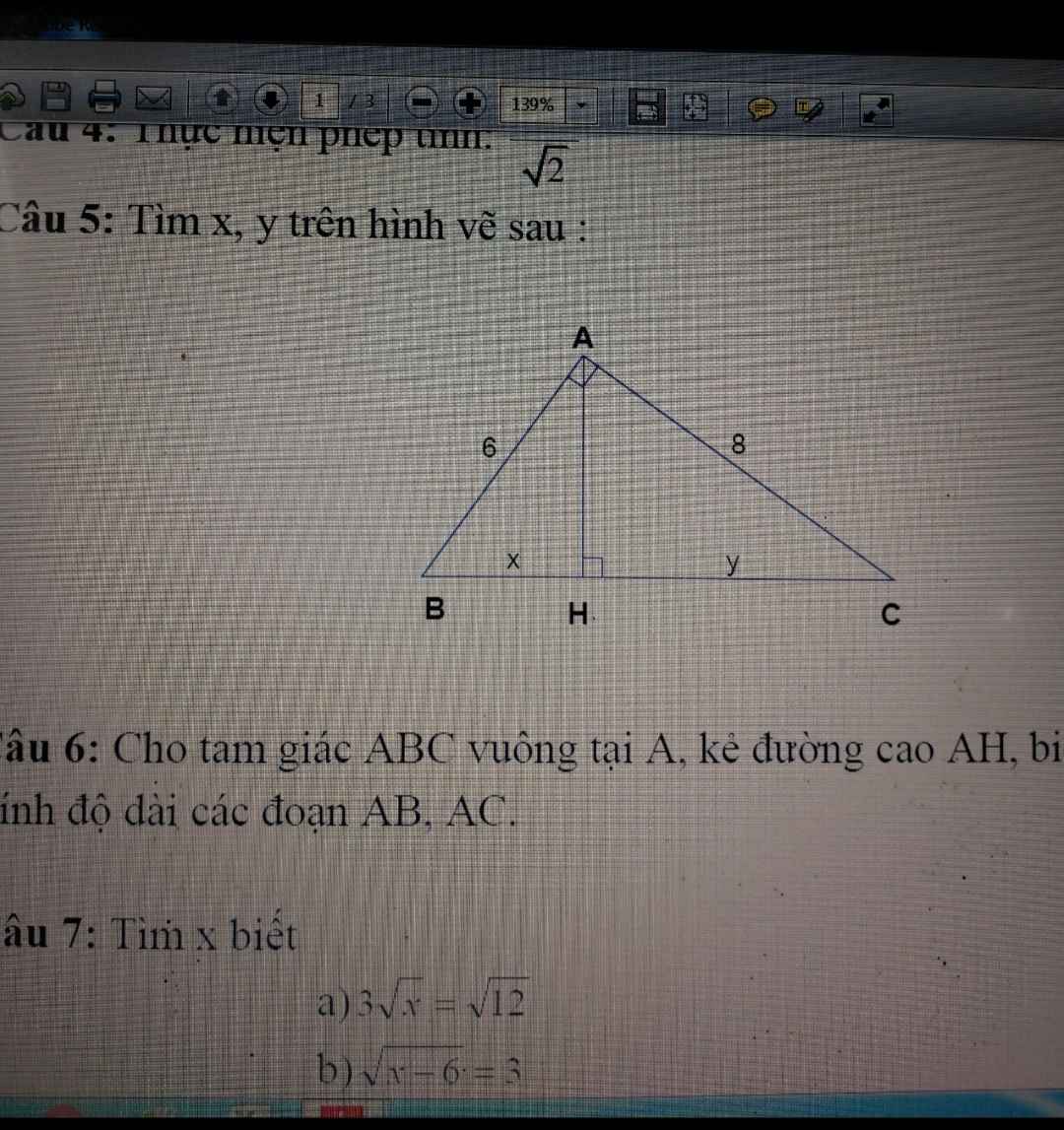
6:
Xét ΔDKE vuông tại K có KA là đường cao
nên \(AD\cdot AE=AK^2\)
Xét ΔDKF vuông tại K có KB là đường cao
nên \(BD\cdot BF=BK^2\)
\(AD\cdot AE+BD\cdot BF\)
\(=AK^2+KB^2=KD^2\)
\(=KE\cdot KF\)
7: Xét ΔDKE vuông tại K có KA là đường cao
nên \(EA\cdot ED=EK^2\)
=>\(EA=\frac{EK^2}{ED}\)
Xét ΔDKF vuông tại K có KB là đường cao
nên \(FB\cdot FD=FK^2\)
=>\(FB=\frac{FK^2}{FD}\)
\(EF\cdot AE\cdot BF=EF\cdot\frac{EK^2}{ED}\cdot\frac{KF^2}{FD}=\frac{EF}{ED\cdot FD}\cdot EK^2\cdot KF^2\)
\(=\frac{EF}{DK\cdot EF}\cdot\left(EK\cdot KF\right)^2=\frac{1}{DK}\cdot DK^4=DK^3\)
\(=AB^3\)