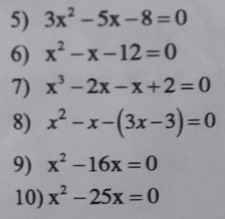Question

Câu 7 giúp mình với ạ :((

Answer 1

Câu 1: 

a: \(=2x^4-6x^2\)

b: \(=3y^2+2\)

Answer 2

Câu 1:

\(a,=2x^4-6x^2\\ b,=3y^2+2\)

Câu 2:

\(\widehat{C}=360^0-55^0-80^0-120^0=105^0\\ \Rightarrow\text{Góc ngoài tại }\widehat{C}=180^0-105^0=75^0\)

Câu 3:

\(a,AM=\dfrac{BC}{2}=\dfrac{\sqrt{AB^2+AC^2}}{2}=\dfrac{15}{2}\left(cm\right)\\ b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot12\cdot9=54\left(cm^2\right)\)

Câu 4:

\(a,=\dfrac{x^2-4x+4}{x-2}=\dfrac{\left(x-2\right)^2}{x-2}=x-2\\ b,=\dfrac{x+1+2x+3-4+x}{6x^2y}=\dfrac{4x}{6x^2y}=\dfrac{2}{3xy}\)

Answer 3

Câu 5:

\(a,=6x\left(y-2x\right)\\ b,=x^2\left(x+y\right)-\left(x+y\right)=\left(x-1\right)\left(x+1\right)\left(x+y\right)\\ c,=3x^2-3x-4x+4=\left(x-1\right)\left(3x-4\right)\)

Câu 6:

Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC

Do đó \(MN=\dfrac{1}{2}BC=5\left(cm\right)\)

Câu 8:

\(a,=\dfrac{5\left(x+y\right)}{\left(x+y\right)^2}=\dfrac{5}{x+y}\\ b,\Rightarrow x\left(x-5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)