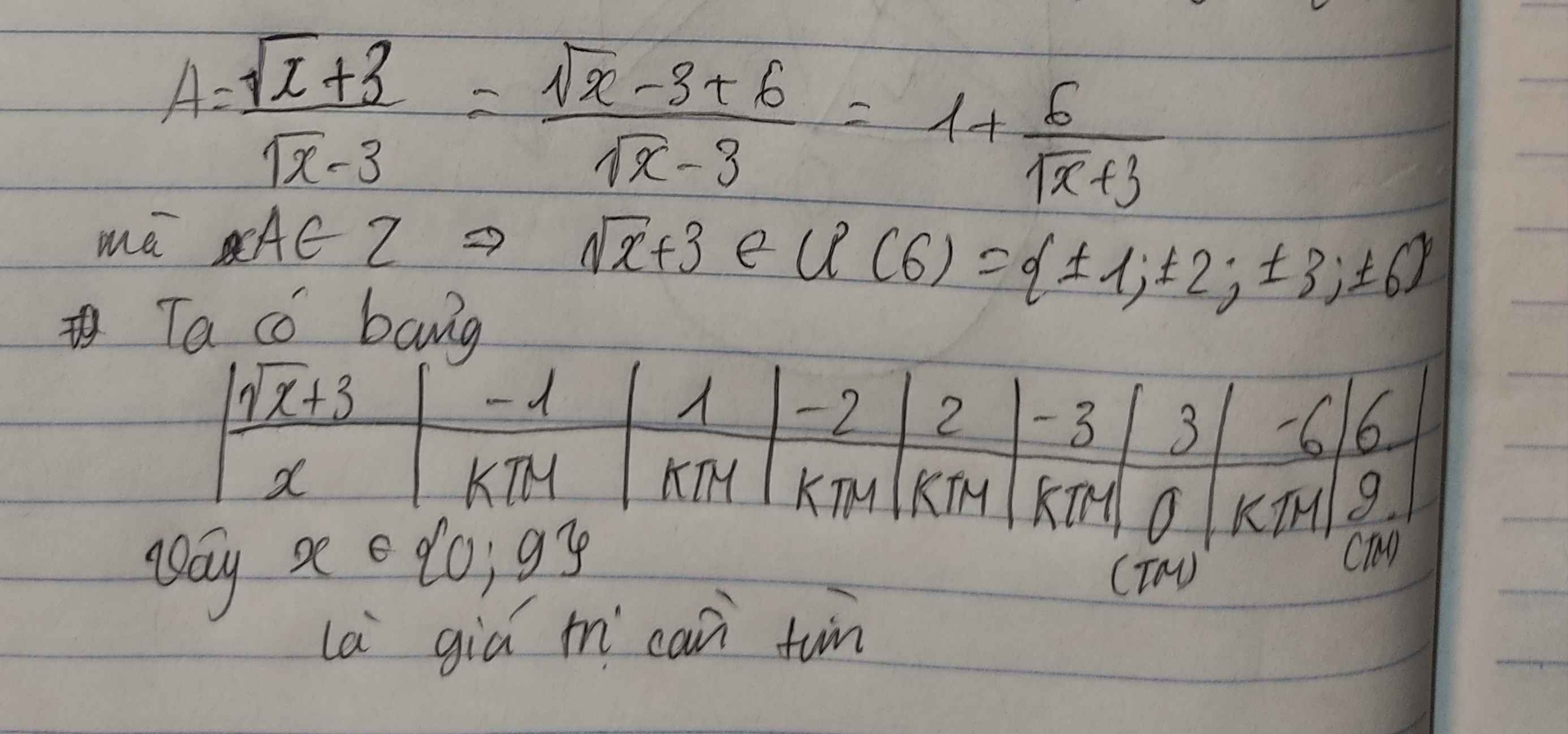Tìm \(x\in R\)để \(\sqrt[3]{3+\sqrt{x}}+\sqrt[3]{3-\sqrt{x}}\in Z\)

Những câu hỏi liên quan
Tìm \(x\in Z\) để \(A=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\in Z-\)
Bài 4:
Cho biểu thức: \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
a) Tìm đkxđ của M và rút gọn
b) Tìm x \(\in Z\) để M \(\in Z\)
\(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\left(\text{đ}k\text{x}\text{đ}:x\ge3\right)\\ =\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\\ =\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{2\sqrt{x}-9-\left(x-9\right)-\left(2x-4\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9-2x+4\sqrt{x}-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{5\sqrt{x}-3x+2}{x-5\sqrt{x}+6}\)
__
Để \(M\in Z\) thì \(x-5\sqrt{x}+6\) thuộc ước của \(5\sqrt{x}-3x+2\)
\(\Rightarrow x-5\sqrt{x}+6=-5\sqrt{x}-3x+2\\ \Leftrightarrow x-5\sqrt{x}+6+5\sqrt{x}+3x-2=0\\ \Leftrightarrow4x-4=0\\ \Leftrightarrow4x=4\\ \Leftrightarrow x=1\)
Đúng 3
Bình luận (1)
Câu 1: \(Q=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{x+5}{x-\sqrt{x}-2}\)
a,Rút gọn Q
b, Tìm \(x\in Z\) để \(Q\in Z\)
1.
\(a,Q=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{x+5}{x-\sqrt{x}-2}\)
\(Q=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)-\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)-x-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ Q=\dfrac{x-3\sqrt{x}+2-x-4\sqrt{x}-3-x-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ Q=\dfrac{-x-7\sqrt{x}-6}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ Q=\dfrac{-\left(x+7\sqrt{x}+6\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ Q=\dfrac{-\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}=\dfrac{-\sqrt{x}-6}{\sqrt{x}-2}\)
\(b,Q\in Z\Leftrightarrow\dfrac{-\sqrt{x}-6}{\sqrt{x}-2}\in Z\)
\(\Leftrightarrow\dfrac{-\left(\sqrt{x}-2\right)-8}{\sqrt{x}-2}\in Z\\ \Leftrightarrow-1-\dfrac{8}{\sqrt{x}-2}\in Z\)
Mà \(-1\in Z\Leftrightarrow\dfrac{8}{\sqrt{x}-2}\in Z\)
\(\Leftrightarrow8⋮\sqrt{x}-2\\ \Leftrightarrow\sqrt{x}-2\inƯ\left(8\right)=\left\{-8,-4,-2,-1,1,2,4,8\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;1;3;4;6;10\right\}\)
Mà \(x\in Z\) và \(\sqrt{x}\ge0\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;4\right\}\\ \Leftrightarrow x\in\left\{0;1;4\right\}\)
Vậy \(x\in\left\{0;1;4\right\}\) thì \(Q\in Z\)
Đúng 1
Bình luận (1)
Cho \(B=\dfrac{2}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
Tìm \(x\in Z\) để B có giá trị nguyên
\(B=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}-2+2\sqrt{x}+x-3\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
Để B nguyên thì \(\sqrt{x}-3\in\left\{1;-1;5\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;8\right\}\)
hay \(x\in\left\{16;4;64\right\}\)
Đúng 0
Bình luận (0)
Cho biểu thức: Q = \(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-3\dfrac{\sqrt{x}-1}{x-5\sqrt{x}+6}\).
a) Tìm điều kiện xác định và rút gọn Q.
b) Tìm các giá trị của x để Q < -1.
c) Tìm các giá trị của x \(\in\) Z sao cho 2Q \(\in\) Z.
a, đk: \(x\ge0,x\ne9,x\ne4\)
\(Q=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-4-x+3\sqrt{x}-\sqrt{x}+3-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2-\sqrt{x}}{-\left(\sqrt{x}-3\right)\left(2-\sqrt{x}\right)}=\dfrac{-1}{\sqrt{x}-3}\)
b,\(Q< -1=>\dfrac{-1}{\sqrt{x}-3}+1< 0< =>\dfrac{-1+\sqrt{x}-3}{\sqrt{x}-3}< 0\)
\(< =>\dfrac{\sqrt{x}-4}{\sqrt{x}-3}< 0\)
\(=>\left\{{}\begin{matrix}\left[{}\begin{matrix}\sqrt{x}-4>0\\\sqrt{x}-3< 0\end{matrix}\right.\\\left[{}\begin{matrix}\sqrt{x}-4< 0\\\sqrt{x}-3>0\end{matrix}\right.\end{matrix}\right.\)\(< =>\left[{}\begin{matrix}\left\{{}\begin{matrix}x>16\\x< 9\end{matrix}\right.\\\left\{{}\begin{matrix}x< 16\\x>9\end{matrix}\right.\end{matrix}\right.\)\(< =>9< x< 16\)
c, \(=>2Q=\dfrac{-2}{\sqrt{x}-3}=1+\dfrac{1}{\sqrt{x}-3}\in Z\)
\(< =>\sqrt{x}-3\inƯ\left(1\right)=\left\{\pm1\right\}\)\(=>x\in\left\{16;4\right\}\)(loại 4)
=>x=16
Đúng 0
Bình luận (0)
a) \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-3\dfrac{\sqrt{x}-1}{x-5\sqrt{x}+6}\)
Ta có \(x-5\sqrt{x}+6=\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)\)
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\\sqrt{x}-3>0\\\sqrt{x}-2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x>9\\x>2\end{matrix}\right.\) \(\Leftrightarrow x>9\)
\(Q=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-3\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\left(x-4\right)-\left(x-2\sqrt{x}-3\right)-\left(3\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\) \(=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\) \(=\dfrac{-\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\) \(=\dfrac{-1}{\left(\sqrt{x}-3\right)}=\dfrac{1}{3-\sqrt{x}}\)
b) \(Q< -1\Leftrightarrow\dfrac{1}{3-\sqrt{x}}< -1\) \(\Leftrightarrow\dfrac{1}{3-\sqrt{x}}+1< 0\) \(\Leftrightarrow\dfrac{4-\sqrt{x}}{3-\sqrt{x}}< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4-\sqrt{x}>0\\3-\sqrt{x}< 0\end{matrix}\right.\\\left\{{}\begin{matrix}4-\sqrt{x}< 0\\3-\sqrt{x}>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 16\\x>9\end{matrix}\right.\\\left\{{}\begin{matrix}x>16\\x< 9\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow9< x< 16\)
Vậy để \(Q< -1\) thì \(S=\left\{x/9< x< 16\right\}\)
c) \(2Q\in Z\Leftrightarrow\dfrac{2}{3-\sqrt{x}}\in Z\)
\(\Rightarrow3-\sqrt{x}\inƯ\left(2\right)\)\(\Leftrightarrow\left\{{}\begin{matrix}3-\sqrt{x}=2\\3-\sqrt{x}=-2\\3-\sqrt{x}=1\\3-\sqrt{x}=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=25\\x=4\\x=16\end{matrix}\right.\)
Kết hợp với ĐKXĐ,ta có để \(2Q\in Z\) thì \(x\in\left\{16;25\right\}\)
Đúng 0
Bình luận (0)
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{9;4\right\}\end{matrix}\right.\)
Ta có: \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{3\sqrt{x}-3}{x-5\sqrt{x}+6}\)
\(=\dfrac{x-4-x+2\sqrt{x}+2-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-1}{\sqrt{x}-3}\)
c) Để 2Q là số nguyên thì \(-2⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;5;1\right\}\)
\(\Leftrightarrow x\in\left\{16;25;1\right\}\)
Đúng 0
Bình luận (0)
Cho biểu thức : \(A=\left(\frac{x-3\sqrt{x}}{x-9}-1\right):\left(\frac{9-x}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}+3}\right)\)
a, Rút gọn A
b, Tìm x để A < 1
c, Tìm \(x\in Z\) để \(A\in Z\)
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\\x\ne9\end{matrix}\right.\)
\(A=\left(\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-1\right):\left(\frac{9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\frac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\\ =\left(\frac{\sqrt{x}-\sqrt{x}-3}{\sqrt{x}+3}\right):\left(\frac{9-x+x-9-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\\ =\frac{-3}{\sqrt{x}+3}:\frac{4-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\frac{-3}{\sqrt{x}+3}\cdot\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{-\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\frac{3}{\sqrt{x}+2}\)
b) Ta có:
\(P=\frac{3}{\sqrt{x}+2}< 1\\ \Leftrightarrow\frac{3}{\sqrt{x}+2}-1< 0\\ \Leftrightarrow\frac{3-\left(\sqrt{x}+2\right)}{\sqrt{x}+2}< 0\\ \Leftrightarrow\frac{1-\sqrt{x}}{\sqrt{x}+2}< 0\\ \Leftrightarrow1-\sqrt{x}< 0\\ \Leftrightarrow\sqrt{x}>1\\ \Leftrightarrow x>1\)
Vậy với \(x>1;x\ne4;x\ne9\)thì P < 1
c) Để \(A\in Z\Leftrightarrow3⋮\sqrt{x}+2\Leftrightarrow\sqrt{x}+2\inƯ\left(3\right)\)
Ta có bảng sau
| \(\sqrt{x}+2\) | 1 | -1 | 3 | -3 |
| \(\sqrt{x}\) | -1 | -3 | 1 | -5 |
| \(x\) | loại | loại | 1(tm) | loại |
Vậy...................
Đúng 0
Bình luận (0)
cho N=\(\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}+\frac{\sqrt{x}+3}{2-\sqrt{x}}\)
a. tìm ĐKXĐ và rút gọn
b.tìm x để N=5
c. tìm x\(\in\)Z để n\(\in\)Z
N=\(\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}+\frac{\sqrt{x}+3}{2-\sqrt{x}}\)
= \(\frac{2\sqrt{x}-9}{x-2\sqrt{x}-3\sqrt{x}+6}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}-\frac{\sqrt{x}+3}{\sqrt{x}-2}\)
= \(\frac{2\sqrt{x}-9}{\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)}+\frac{2\sqrt{x}+1}{\left(\sqrt{x}-3\right)}-\frac{\sqrt{x}+3}{\sqrt{x}-2}\)
= \(\frac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\frac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
ĐKXĐ : x ≠ 4 ; x ≠ 9
Rút gọn :
=\(\frac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\frac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
= \(\frac{2\sqrt{x}-9+\left(\sqrt{x}-2\right)\left(2\sqrt{x}+1-\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
=\(\frac{2\sqrt{x}-9+\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
= \(\frac{2\sqrt{x}-9+x-2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
= \(\frac{x-5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
Để N =5 thì :
<=> \(\frac{x-5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\) =5
<=> x-5 = \(\left(5\sqrt{x}-10\right)\left(\sqrt{x}-3\right)\)
<=> x-5 = 5x - \(15\sqrt{x}\) - \(10\sqrt{x}\) +30
<=> x-5x-25\(\sqrt{x}\) =35
Đúng 0
Bình luận (2)
a) \(\sqrt{x}\ne3;\sqrt{x}\ne2\Rightarrow x\ne4;x\ne9\)
\(N=\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}+\frac{\sqrt{x}+3}{2-\sqrt{x}}\)
\(\Leftrightarrow N=\frac{2\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}-\frac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(\Leftrightarrow N=\frac{2\sqrt{x}-9+2x-3\sqrt{x}-2-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(\Rightarrow N=\frac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
b) \(N=5\Leftrightarrow\frac{\sqrt{x}+1}{\sqrt{x}-3}=5\)
\(\Leftrightarrow\sqrt{x}+1=5\sqrt{x}-15\Leftrightarrow4\sqrt{x}=16\)
\(\Leftrightarrow\sqrt{x}=4\Rightarrow x=16\) (thỏa mãn)
c) \(N=\frac{\sqrt{x}+1}{\sqrt{x}-5}=\frac{\sqrt{x}-5+6}{\sqrt{x}-5}=1+\frac{6}{\sqrt{x}-5}\)
để N \(\in\) Z thì \(\left(\sqrt{x}-5\right)\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| \(\sqrt{x}-5\) | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| x | 36 | 16 | 49 | 9 | 64 | 4 | 121 | loại |
Đúng 0
Bình luận (2)
a. ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\\x\ne9\end{matrix}\right.\)
\(N=\frac{2\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\frac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\\ =\frac{2\sqrt{x}-9+2x-4\sqrt{x}+\sqrt{x}-2-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ =\frac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ =\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ =\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
b.
\(N=\frac{\sqrt{x}+1}{\sqrt{x}-3}=5\\ \Leftrightarrow\sqrt{x}+1=5\left(\sqrt{x}-3\right)\\ \Leftrightarrow\sqrt{x}+1=5\sqrt{x}-15\\ \Leftrightarrow4\sqrt{x}=16\\ \Leftrightarrow\sqrt{x}=4\Leftrightarrow x=16\left(tm\right)\)
c.
\(N=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)
Để \(N\in Z\Leftrightarrow4⋮\sqrt{x}-3\Leftrightarrow\sqrt{x}-3\inƯ\left(4\right)\)
Ta có bảng sau:
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| \(\sqrt{x}\) | 4 | 2 | 5 | 1 | 7 | -1 |
| \(x\) | 16(tm) | 4(loại) | 25(tm) | 1(tm) | 49(tm) | loại |
Vậy......
Đúng 0
Bình luận (1)
Q = \(\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}-\frac{2\sqrt{x}+1}{3-\sqrt{x}}\)với đk x \(\ge0,x\ne9,x\ne4\)
1. rút gọn Q
2. tìm x để Q < 1
3. tìm x \(\in\)Z để Q\(\in\)Z
Cho biểu thức : \(A=\left(\frac{x-3\sqrt{x}}{x-9}-1\right):\left(\frac{9-x}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}+3}\right)\)
a, Rút gọn A
b, Tìm x để A < 1
c, Tìm \(x\in Z\) để \(A\in Z\)
\(ĐKXĐ:\)
\(\hept{\begin{cases}x-9\ne0\\\sqrt{x}-2\ne0\\\sqrt{x}+3\ne0;x\ge0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ne9\\x\ne4\\x\ge0\end{cases}}\)
Vậy...................................................
Đúng 0
Bình luận (0)
\(A=\left(\frac{x-3\sqrt{x}}{x-9}-1\right):\left(\frac{9-x}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}+3}\right)\)
\(=\left(\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-1\right):\left(\frac{9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}+3}\right)\)
\(=\frac{\sqrt{x}-\sqrt{x}-3}{\left(\sqrt{x}+3\right)}:\left(\frac{9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\frac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)
\(=\frac{-3}{\sqrt{x}+3}:\left(\frac{9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\frac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\frac{x-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)
\(=\frac{-3}{\sqrt{x}+3}:\frac{9-x+x-9-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{-3}{\sqrt{x}+3}:\frac{-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{-3}{\sqrt{x}+3}.\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{4-x}\)
\(=\frac{3\left(2-\sqrt{x}\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
\(=\frac{3}{\left(2+\sqrt{x}\right)}\)
Đúng 0
Bình luận (0)
Đế A<1 \(\Rightarrow\frac{3}{2+\sqrt{x}}< 1\)
\(\Leftrightarrow\frac{3}{2+\sqrt{x}}-1< 0\)
\(\Leftrightarrow\frac{3-2-\sqrt{x}}{2+\sqrt{x}}< 0\)
\(\Leftrightarrow\frac{1-\sqrt{x}}{2+\sqrt{x}}< 0\)
Vì \(2+\sqrt{x}>0\forall x\in R\)
\(\Rightarrow1-\sqrt{x}< 0\)
\(\Leftrightarrow\sqrt{x}>1\Leftrightarrow x>1\)
Kết hợp ĐKXĐ \(\Rightarrow\hept{\begin{cases}x>1\\x\ne4\\x\ne9\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời