Đồ thị hàm số y=x2 đi qua hai điểm (\(\sqrt{2}\);m)và(-\(\sqrt{3}\);n).Khi đó giá trị của biểu thức m2-n2 bằng
A.5 B.-1 C.1 D.-5
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Xác định hàm số y=ax+b trong mỗi trường hợp sau:
a) Khi a=\(\sqrt{3}\), đồ thị hàm số cắt trục tung tại điểm có tung độ bằng _ \(\sqrt{3}\)
b) Khi a= -5 , đồ thị hàm số đi qua điểm A(-2;3)
c) Đồ thị hàm số đi qua hai điểm M(1;3) và N(-2;6)
d) Đồ thị hàm số song song với đường thẳng y=\(\sqrt{7}x\) và đi qua điểm (1;7+\(\sqrt{7}\))
Cho hàm số y = (m-3)x +2021 (m ≠ 3) (1)
a, Tìm m để đồ thị hàm số (1) đi qua A(1;2025)
b, Timg m để đồ thị hàm số (1) cắt (P): y= -x2 tại hai điểm phân biệt
a) Vì đồ thị hàm số (1) đi qua A(1;2025) nên ta có:
\(\left(m-3\right)1+2021=2025\\ \Leftrightarrow m-3=4\\ \Leftrightarrow m=7\)
Bài 1 :Cho hàm số y=(m-1)x+m+3
1, Tìm giá trị của m để đồ thị hàm số song song với đồ thị hàm số y=-2x+1
2, Tìm giá trị của m để đồ thị hàm số đi qua điểm (1;-4)
3, Tìm điểm cố định mà đồ thị của hàm số luôn đi qua\
Bài 2 : Cho hàm số y=(2m-1)x+m-3
1, Tìm m để đồ thị hàm số đi qua điểm (2;5)
2, Cmr đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m. Tìm điểm cố định ấy
3, Tìm m để đồ thị hàm số cắt trục hoành tai điểm có hoành độ \(x=\sqrt{2}-1\)
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x 2 + 2 x x − 1
A. y = − 2 x − 2
B. y = 2 x + 2
C. y = 2 x − 2
D. y = − 2 x + 2
Đáp án B
y = x 2 + 2 x x − 1
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là
y = x 2 + 2 x ' x − 1 ' = 2 x + 2
Hàm số bậc hai y = a x 2 + b x - 6 có đồ thị đi qua hai điểm A(1; 1) và B(2; 2) là
A. y = 2 x 2 + 5x - 6
B. y = -3 x 2 + 10x - 6
C. y = -2 x 2 + 8x - 6
D. y = 3 x 2 + 3x - 6
Xác định hàm số y = a x 2 và vẽ đồ thị của nó, biết rằng đồ thị của nó đi qua điểm A (-1; 2).
Đồ thị hàm số đi qua A (-1; 2) nên tọa độ của A nghiệm đúng phương trình hàm số: 2 = a - 1 2 } ⇔ a = 2
Hàm số đã cho: y = 2 x 2
Vẽ đồ thị hàm số: y = 2 x 2
x |
-2 |
-1 |
0 |
1 |
2 |
| y = 2 x 2 | 8 |
2 |
0 |
2 |
8 |
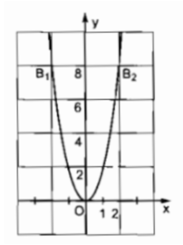
Đồ thị hàm số y = 1/3 x 2 đi qua điểm nào sau đây?
A. A(1; 0)
B. B 1 3 ; 1 27
C. C 1 3 ; 1 9
D. D 1 4 ; 1 16
tìm a và b biết đồ thị hàm số y=ax+b đi qua các điểm (\(\sqrt{2}\); 4-\(\sqrt{2}\))và (2;\(\sqrt{2}\))
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot\sqrt{2}+b=4-\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\left(\sqrt{2}-2\right)=4-2\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{4-2\sqrt{2}}{\sqrt{2}-2}=-2\\b=\sqrt{2}+4\end{matrix}\right.\)
Xác định hàm số bậc nhất \(y=ax+b\) trong mỗi trường hợp sau :
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5
b) a = 3 và đồ thị của hàm số đi qua điểm A( 2; 2)
c) Đồ thị của hàm số song song với đường thẳng \(y=\sqrt{3}x\) và đi qua điểm \(B\left(1;\sqrt{3}+5\right)\)
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.
Bài giải:
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.