Giúp em nhanh với ạ vì sáng mai em nộp r ạ. Em cảm ơn rất nhiều ạ

Những câu hỏi liên quan
Làm nhanh giúp em vs ạ, sáng mai em nộp r ạ. Em ảm ơn rất nhiều
19
Từ pt đầu ta có:
\(x^2-xy-2xy+2y^2=0\)
\(\Leftrightarrow x\left(x-y\right)-2y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=2y\end{matrix}\right.\)
TH1: \(x=y\) thế xuống pt dưới:
\(y^2-y-y^2=1\Rightarrow y=-1\Rightarrow x=-1\)
TH2: \(x=2y\) thế xuống pt dưới:
\(\left(2y\right)^2-2y-y^2=1\Leftrightarrow3y^2-2y-1=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-\dfrac{1}{3}\Rightarrow x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(-1;-1\right);\left(1;2\right);\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)\)
Đúng 2
Bình luận (0)
21.
Từ pt đầu:
\(xy+2=2x+y\Leftrightarrow xy-y+2-2x=0\)
\(\Leftrightarrow y\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(y-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
TH1: \(x=1\) thế xuống pt dưới:
\(2y+y^2+3y=6\Leftrightarrow y^2+5y-6=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-6\end{matrix}\right.\)
TH2: \(y=2\) thế xuông pt dưới
\(4x+4+6=6\Rightarrow x=-1\)
Vậy nghiệm của pt là: \(\left(x;y\right)=\left(1;1\right);\left(1;-6\right);\left(-1;2\right)\)
Đúng 2
Bình luận (0)
22.
\(\Leftrightarrow\left\{{}\begin{matrix}9x^2-6xy+y^2+6xy=10\\\left(3x-y\right)\left(10-6xy\right)=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3x-y\right)^2=10-6xy\\\left(3x-y\right)\left(10-6xy\right)=8\end{matrix}\right.\)
Thế \(10-6xy\) từ pt trên xuống dưới ta được
\(\left(3x-y\right)\left(3x-y\right)^2=8\)
\(\Leftrightarrow\left(3x-y\right)^3=2^3\)
\(\Leftrightarrow3x-y=2\)
\(\Leftrightarrow y=3x-2\)
Thế vào pt đầu:
\(9x^2+\left(3x-2\right)^2=10\)
\(\Leftrightarrow18x^2-12x-6=0\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-\dfrac{1}{3}\Rightarrow y=-3\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
E cần gấp ạ! Hơi nhiều nhưng mong a chị giúp em vì ngày mai là hạn nộp ạ! Em cảm ơn 



Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
Đọc tiếp
 Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
E biết là hơi nhiều ạ! Mong a chị giúp em vì ngày mai là hạn nộp rồi ạ! E cảm ơn nhiều 


Em đăng tách ra 1 lần 5-7 câu thôi he!
Đúng 0
Bình luận (0)
Anh chị giúp e câu toán 9 với ạ .Ngày mai e kt giữa kì r .Em cảm ơn rất nhiều luôn ạ
a: \(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{2\sqrt{x}+2+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}}{x-1}\)
Đúng 0
Bình luận (0)
\(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{2\left(\sqrt{x}+1\right)+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{x+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt{3+2\sqrt{2}}}{3+2\sqrt{2}-1}\)
\(\Rightarrow P=\dfrac{\sqrt{\left(\sqrt{2}+1\right)^2}}{2+2\sqrt{2}}\)
\(\Rightarrow P=\dfrac{\sqrt{2}+1}{2\left(\sqrt{2}+1\right)}\)
\(\Rightarrow P=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Mọi người ơi, giúp em nhanh bài này với ạ, em đang cần gấp lắm ạ. Em cảm ơn rất nhiều ạ!!!!!

ANH CHỊ ƠI GIÚP EM MẤY CÂU TOÁN LỚP 9 VỚI Ạ, MAI EM THI RỒI , EM CẢM ƠN RẤT NHIỀU Ạ❤
Câu 1:
Ta có 2x - y = 8 => 2x - y + 9 = 17
Mà 3x + y = 17 => 2x - y + 9 = 3x + y
<=> 9 - y = x + y <=> 9 = x + 2y <=> x = 9 - 2y
Mà 2x - y = 8 => 18 - 4y - y = 8 => 18 - 5y = 8 => y = 2 => x = 5
Đúng 1
Bình luận (1)
Mọi người giúp mình câu 123 với an mình
Cảm ơn rất nhiều ạ mình cần gấp vì mai phải nộp ạ

ANH CHỊ ƠI GIÚP EM 2 BÀI TOÁN LỚP 7 VỚI Ạ .MAI EM KIỂM TRA GIỮA KÌ RỒI .EM CẢM ƠN RẤT NHIỀU Ạ.
Bài 2:
\(\dfrac{1}{2}:\dfrac{5}{4}=x:\dfrac{10}{3}\Leftrightarrow\dfrac{1}{2}.\dfrac{4}{5}=\dfrac{3}{10}x\Leftrightarrow\dfrac{3}{10}x=\dfrac{2}{5}\Leftrightarrow x=\dfrac{2}{5}:\dfrac{3}{10}=\dfrac{4}{3}\)
Bài 3:
Áp dụng t/c dtsbn:
\(\dfrac{x}{4}=\dfrac{y}{12}=\dfrac{x+y}{4+12}=\dfrac{48}{16}=3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.4=12\\y=3.12=36\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Dạ giúp em ạ E cảm ơn nhanh ạ vì btvn của em phải nộp trong tối 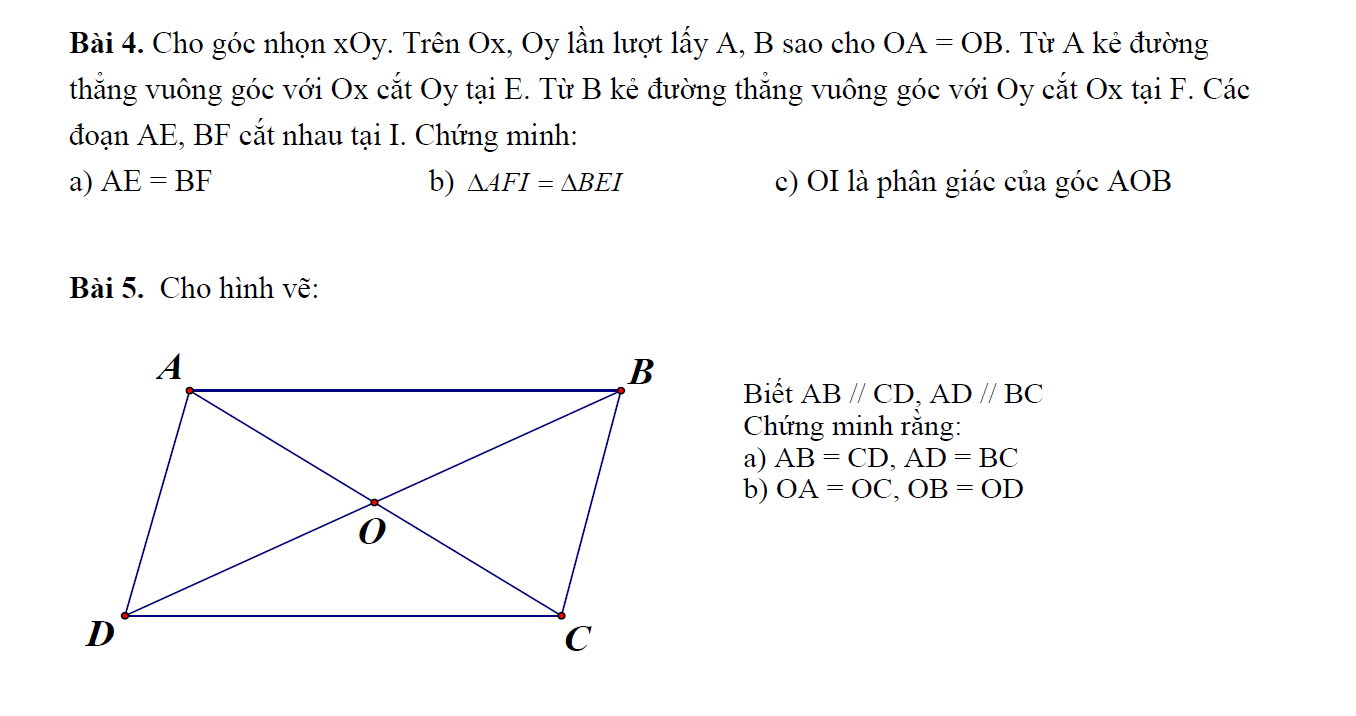 =)))
=)))